Question

如图：BC⊥AD，垂足为D．若∠A=21°，∠B=42°，求∠C和∠AEF的度数．

Answer 1

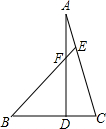解：∵如图：BC⊥AD，
∴∠ADC=90°．
∵∠A=21°，
∴∠C=180°-90°-∠A=69°．
又∵∠AEF=∠B+∠C，∠B=42°，
∴∠AEF=69°+42°=111°．
分析：利用“Rt△ADC的内角和是180°”的性质求得∠C=69°；然后由△BCE的外角性质来求∠AEF的度数．
点评：本题考查了三角形的外角性质，三角形内角和定理．当然了，此题也可以根据“直角三角形的两个锐角互余”的性质来求∠C的度数．