题目内容
如图，正五边形ABCDE中，DC和AB的延长线交于F，则图中与△DBF相似的三角形有（不再添加其他的线段和字母，不包括△DBF本身）
- A.1个
- B.2个
- C.3个
- D.4个
B
分析：由于五边形ABCDE是正五边形，那么有∠E=∠BCD=108°，AB=BC=CD=DE=AE，AD=BD，易求∠DAB=∠DBA=72°，进而可求∠DBF、∠F，从而可得∠E=∠BCD=∠DBF，∠EAD=∠EDA=∠BDC=∠CBD=∠F，从而可证△DEA∽△DCB∽△DBF．
解答：
解：∵五边形ABCDE是正五边形，
∴∠E=∠BCD=108°，AB=BC=CD=DE=AE，AD=BD，
∴∠EAD=∠EDA=∠BDC=∠CBD=
=36°，
∴∠DAB=∠DBA=72°，
∴∠DBF=180°-72°=108°，∠F=36°，
∴∠E=∠BCD=∠DBF，∠EAD=∠EDA=∠BDC=∠CBD=∠F，
∴△DEA∽△DCB∽△DBF．
故选B．
点评：本题考查了五边形内角和计算、三角形内角和定理、相似三角形的判定和性质．解题的关键是求出关键角的度数．
分析：由于五边形ABCDE是正五边形，那么有∠E=∠BCD=108°，AB=BC=CD=DE=AE，AD=BD，易求∠DAB=∠DBA=72°，进而可求∠DBF、∠F，从而可得∠E=∠BCD=∠DBF，∠EAD=∠EDA=∠BDC=∠CBD=∠F，从而可证△DEA∽△DCB∽△DBF．
解答：
解：∵五边形ABCDE是正五边形，∴∠E=∠BCD=108°，AB=BC=CD=DE=AE，AD=BD，
∴∠EAD=∠EDA=∠BDC=∠CBD=
=36°，∴∠DAB=∠DBA=72°，
∴∠DBF=180°-72°=108°，∠F=36°，
∴∠E=∠BCD=∠DBF，∠EAD=∠EDA=∠BDC=∠CBD=∠F，
∴△DEA∽△DCB∽△DBF．
故选B．
点评：本题考查了五边形内角和计算、三角形内角和定理、相似三角形的判定和性质．解题的关键是求出关键角的度数．
练习册系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
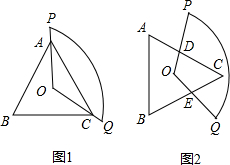
如图，若五边形ABCDE是⊙O的内接正五边形，则∠BOC=
