Question

【题目】如图，已知在矩形ABCD中，BC=2CD=2a，点E在边CD上，在矩形ABCD的左侧作矩形ECGF，使CG=2GF=2b，连接BD，CF，连结AF交BD于点H．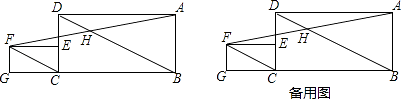

（1）求证：BD∥CF；
（2）求证：H是AF的中点；
（3）连结CH，若HC⊥BD，求a：b的值．

Answer 1

【答案】
（1）解：∵四边形ABCD、四边形ECGF均为矩形，

∴∠G=∠DCB=90°．

∵BC=2CD=2a，CG=2GF=2b，

∴ ．

∴△FGC∽△DCB．

∴∠FCG=∠DBC．

∴BD∥CF．

（2）解：如图1所示：连接AC，交BD于点O．

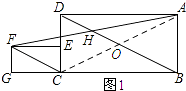
∵四边形ABCD为矩形，

∴OC=OA．

又∵FC∥BD，

∴HF=AH．

∴点H是AF的中点．

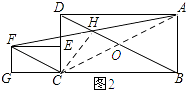
（3）解：如图2所示：连接CH，CA，AC与BD交于点O．

由勾股定理可知：FC= b，AC= a．

∵四边形ABCD为矩形，

∴DB=AC= a，CO= AC= ．

∵HO是△AFC的中位线，

∴HO= FC= ．

∵ ，

∴CH= ．

在△COH中，由勾股定理可知：HO2+CH2=OC2，即（ ）2+（ ）2=（ ）2．

整理得：a2= ．

∴a：b= ．

【解析】（1）根据矩形的性质得出∠G=∠DCB，再根据已知BC=2CD=2a，CG=2GF=2b，得出两边对应成比例，因此可证明△FGC∽△DCB．得出对应角相等，即可证得结论。
（2）连接AC，交BD于点O．根据矩形的性质得出OC=OA．再根据平行线等分线段定理，即可得出结论。
（3）连接CH，CA，AC与BD交于点O．由勾股定理求出FC、AC的长，再根据矩形的对角线相等且互相平分，求得CO的长，然后根据三角形的中位线定理求出HO的长，又由直角三角形的两个面积公式得出CH的长，在△COH中，由勾股定理可求得a：b的值。
【考点精析】本题主要考查了勾股定理的概念和三角形中位线定理的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半才能正确解答此题．