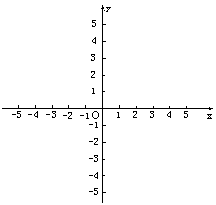��Ŀ����
��֪������ ��ͼ������ƽ��m����λ��
��ͼ������ƽ��m����λ��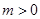 ���õ����������߹��㣨1��8��.
���õ����������߹��㣨1��8��.
��1����m��ֵ������ƽ�ƺ�������߽���ʽд��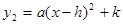 ����ʽ��
����ʽ��
��2����ƽ�ƺ����������x���·��IJ�����x�ᷭ�۵�x���Ϸ�����ƽ�ƺ��������û�б仯�IJ��ֹ���һ���µ�ͼ��. ��д�����ͼ���Ӧ�ĺ���y�Ľ���ʽ��ͬʱд���ú����� ��
��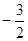 ʱ��Ӧ�ĺ���ֵy��ȡֵ��Χ��
ʱ��Ӧ�ĺ���ֵy��ȡֵ��Χ��
��3����һ�κ���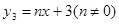 �����Ƿ����������
�����Ƿ����������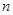 ʹ�ã�2���к����ĺ���ֵ
ʹ�ã�2���к����ĺ���ֵ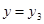 ʱ����Ӧ��x��ֵΪ
ʱ����Ӧ��x��ֵΪ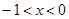 �������ڣ����
�������ڣ���� ��ֵ���������ڣ�˵������.
��ֵ���������ڣ�˵������.
���𰸡�
�⣺��1��������ɵ�
�ֵ㣨1��8����ͼ����
�� 
�� m=2
�� 
��2��
�� ʱ��
ʱ��
��3��������
���ɣ���y=y3�Ҷ�Ӧ��-1<x<0ʱ��

��  ��
��
�� ��
��
�� ������������n��������
����������1������������y1=x2+4x+1��ͼ������ƽ��m����λ���ɵ�y2=x2+4x+1+m���������ֵ㣨1��8����ͼ���ϣ����m���ɣ�
��2�����ݺ�������ʽ����ͼ���ɵó�������С�ֽ�㣻
��3�����ݵ�y=y3�Ҷ�Ӧ�ĩ�1��x��0ʱ��x2+4x+3=nx+3���ó�nȡֵ��Χ���ɵó��𰸣�

��ϰ��ϵ�д�
 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
�����Ŀ
 ��֪��������y=��m-1��x2+mx+m2-4��ͼ��ԭ�㣬�ҿ������ϣ�
��֪��������y=��m-1��x2+mx+m2-4��ͼ��ԭ�㣬�ҿ������ϣ�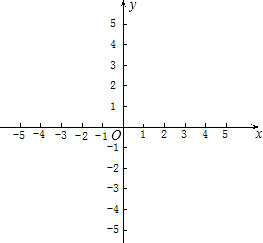 ���ĺ���ֵy=y3ʱ����Ӧ��x��ֵΪ-1��x��0�������ڣ����n��ֵ���������ڣ�˵�����ɣ�
���ĺ���ֵy=y3ʱ����Ӧ��x��ֵΪ-1��x��0�������ڣ����n��ֵ���������ڣ�˵�����ɣ� ��ͼ������ƽ��m����λ��
��ͼ������ƽ��m����λ�� ���õ����������߹��㣨1��8��.
���õ����������߹��㣨1��8��. ����ʽ��
����ʽ��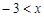 ��
��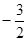 ʱ��Ӧ�ĺ���ֵy��ȡֵ��Χ��
ʱ��Ӧ�ĺ���ֵy��ȡֵ��Χ��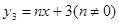 �����Ƿ����������
�����Ƿ����������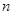 ʹ�ã�2���к����ĺ���ֵ
ʹ�ã�2���к����ĺ���ֵ ʱ����Ӧ��x��ֵΪ
ʱ����Ӧ��x��ֵΪ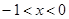 �������ڣ����
�������ڣ����