题目内容
如图是一张“3×5”(表示边长分别为3和5)的长方形,现要把它分成若干张边长为整数的长方形(包括正方形)纸片,并要求分得的任何两张纸片都不完全相同.
(1)能否分成5张满足上述条件的纸片?
(2)能否分成6张满足上述条件的纸片?
若能分,用“a×b”的形式分别表示出各张纸片的边长,并画出分割的示意图;若不能分,请说明理由.

(1)能否分成5张满足上述条件的纸片?
(2)能否分成6张满足上述条件的纸片?
若能分,用“a×b”的形式分别表示出各张纸片的边长,并画出分割的示意图;若不能分,请说明理由.

分析:(1)首先把“3×5”的长方形分割成所有若干张边长为整数的长方形(包括正方形)纸片,再进一步灵活拼凑即可找出解决问题的方案;
(2)利用(1)中分割后的图形进一步分析讨论解决问题.
(2)利用(1)中分割后的图形进一步分析讨论解决问题.
解答:解:(1)把可分得的边长为整数的长方形按面积从小到大排列,
由1×1,1×2,1×3,1×4,2×2,1×5,2×3,2×4,3×3,2×5,3×4,3×5,若能分成5张满足条件的纸片,
因为其面积之和为15,所以买足条件的有1×1,1×2,1×3,1×4,1×5(如图①)
或1×1,1×2,1×3,2×2,1×5(如图②);
① ②
②
(2)若能分成6张满足条件的纸片,则其面积之和仍应为15,但上面排在前列的6个长方形的面积之和为1×1+1×2+1×3+1×4+2×2+1×5=19>15,所以分成6张满足条件的纸片是不可能的.
由1×1,1×2,1×3,1×4,2×2,1×5,2×3,2×4,3×3,2×5,3×4,3×5,若能分成5张满足条件的纸片,
因为其面积之和为15,所以买足条件的有1×1,1×2,1×3,1×4,1×5(如图①)
或1×1,1×2,1×3,2×2,1×5(如图②);
①
 ②
②
(2)若能分成6张满足条件的纸片,则其面积之和仍应为15,但上面排在前列的6个长方形的面积之和为1×1+1×2+1×3+1×4+2×2+1×5=19>15,所以分成6张满足条件的纸片是不可能的.
点评:此题主要利用图形的分割与拼凑解答问题,在具体的解答过程中抓住边长为整数的长方形的面积分析与选择.

练习册系列答案
相关题目
 3、如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=( )
3、如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=( ) 4、如图是一张卡通图,图中两圆的位置关系是( )
4、如图是一张卡通图,图中两圆的位置关系是( ) 16、如图是一张长9cm、宽5cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,可制成底面积是12cm2的一个无盖长方体纸盒,设剪去的正方形边长为xcm,则可列出关于x的方程为
16、如图是一张长9cm、宽5cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,可制成底面积是12cm2的一个无盖长方体纸盒,设剪去的正方形边长为xcm,则可列出关于x的方程为 如图是一张月历,请解决下列问题:
如图是一张月历,请解决下列问题: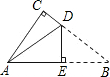 如图是一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为
如图是一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为