题目内容
 九年级某班开展数学活动,活动内容为测量如图所示的电杆AB的高度.在太阳光的照射下,电杆影子的一部分(BE)落在地面上,另一部分(EF)落在斜坡上,站在水平面上的小明的影子为DG,已知斜坡的倾角∠FEH=30°,CD=1.6m,DG=0.8m,BE=2.1m,EF=1.7m,则电杆的高是多少?(精确到0.1,参考数据:
九年级某班开展数学活动,活动内容为测量如图所示的电杆AB的高度.在太阳光的照射下,电杆影子的一部分(BE)落在地面上,另一部分(EF)落在斜坡上,站在水平面上的小明的影子为DG,已知斜坡的倾角∠FEH=30°,CD=1.6m,DG=0.8m,BE=2.1m,EF=1.7m,则电杆的高是多少?(精确到0.1,参考数据:| 2 |
| 3 |
分析:首先延长AF交BH于点N,过点F作FM⊥BH于点M,利用同一时刻实际物体与影长的关系得出MN以及BN的长,进而得出AB的长即可.
解答:解:延长AF交BH于点N,过点F作FM⊥BH于点M,
∵∠FEH=30°,EF=1.7m,
∴FM=0.85m,
∴EM=
×1.7
≈1.47,
由题意可得出:AB∥FM,
∴
=
,
∵CD=1.6m,DG=0.8m,
∴MN=0.68m,
∵BE=2.1m,
∴BN=2.1+1.47+0.68=4.25(m),
∵
=
,
∴
=
,
解得:AB≈5.3(m).
答:电杆的高约为5.3m.
∵∠FEH=30°,EF=1.7m,
∴FM=0.85m,
∴EM=
| 1 |
| 2 |
| 3 |

由题意可得出:AB∥FM,
∴
| FM |
| MN |
| CD |
| DG |
∵CD=1.6m,DG=0.8m,
∴MN=0.68m,
∵BE=2.1m,
∴BN=2.1+1.47+0.68=4.25(m),
∵
| AB |
| BN |
| CD |
| DG |
∴
| AB |
| 4.25 |
| 1 |
| 0.8 |
解得:AB≈5.3(m).
答:电杆的高约为5.3m.
点评:此题主要考查了解直角三角形的应用,根据实际物体与影长之间的关系得出是解题关键.

练习册系列答案
相关题目
 九年级某班开展数学活动,活动内容为测量如图所示的电杆AB的高度.在太阳光的照射下,电杆影子的一部分(BE)落在地面上,另一部分(EF)落在斜坡上,站在水平面上的小明的影子为DG,已知斜坡的倾角∠FEH=30°,CD=1.6m,DG=0.8m,BE=2.1m,EF=1.7m,则电杆的高约为
九年级某班开展数学活动,活动内容为测量如图所示的电杆AB的高度.在太阳光的照射下,电杆影子的一部分(BE)落在地面上,另一部分(EF)落在斜坡上,站在水平面上的小明的影子为DG,已知斜坡的倾角∠FEH=30°,CD=1.6m,DG=0.8m,BE=2.1m,EF=1.7m,则电杆的高约为 九年级某班开展数学活动,活动内容为测量如图所示的电杆AB的高度.在太阳光的照射下,电杆影子的一部分(BE)落在地面上,另一部分(EF)落在斜坡上,站在水平面上的小明的影子为DG,已知斜坡的倾角∠FEH=30°,CD=1.6m,DG=0.8m,BE=2.1m,EF=1.7m,则电杆的高约为________m.(精确到0.1,参考数据:
九年级某班开展数学活动,活动内容为测量如图所示的电杆AB的高度.在太阳光的照射下,电杆影子的一部分(BE)落在地面上,另一部分(EF)落在斜坡上,站在水平面上的小明的影子为DG,已知斜坡的倾角∠FEH=30°,CD=1.6m,DG=0.8m,BE=2.1m,EF=1.7m,则电杆的高约为________m.(精确到0.1,参考数据: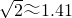 ,
, )
) ≈1.41,
≈1.41, ≈1.73)
≈1.73)
 ,
, )
)