题目内容
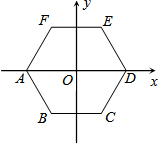如图，将正六边形ABCDEF放在平面直角坐标系中，中心与坐标原点重合，若D点的坐标为（1，0），那么点C的坐标为________．
（
，-
）
分析：连接OC，由于正六边形的中心角是60°，则△COD是等边三角形，OC=1，设BC交y轴于G，那么∠GOC=30°，然后解Rt△GOC，求出GC与OG的值，进而得到点C的坐标．
解答：
解：连接OC．
∵∠COD=
=60°，OC=OD，
∴△COD是等边三角形，
∴OC=OD=1．
设BC交y轴于G，则∠GOC=30°．
在Rt△GOC中，∵∠GOC=30°，OC=1，
∴GC=，OG=．
∴C（，-）．
故答案为：（，-）．
点评：本题考查了正六边形和圆，坐标与图形性质，解直角三角形，难度适中．得出OC=1，∠GOC=30°是解题的关键．
，-）分析：连接OC，由于正六边形的中心角是60°，则△COD是等边三角形，OC=1，设BC交y轴于G，那么∠GOC=30°，然后解Rt△GOC，求出GC与OG的值，进而得到点C的坐标．
解答：
解：连接OC．∵∠COD=
=60°，OC=OD，∴△COD是等边三角形，
∴OC=OD=1．
设BC交y轴于G，则∠GOC=30°．
在Rt△GOC中，∵∠GOC=30°，OC=1，
∴GC=
，OG=．∴C（
，-）．故答案为：（
，-）．点评：本题考查了正六边形和圆，坐标与图形性质，解直角三角形，难度适中．得出OC=1，∠GOC=30°是解题的关键．
练习册系列答案
相关题目
如图，将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动，当A1第一次滚动到图2位置时，顶点A1所经过的路径的长为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
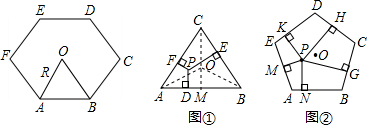（2012•青岛模拟）同学们已经认识了很多正多边形，现以正六边形为例再介绍与正多边形相关的几个概念．如正六边形ABCDEF各边对称轴的交点O，又称正六边形的中心，其中OA称正六边形的半径，通常用R表示，∠AOB称为中心角，显然．提出问题：正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系？
πa
πa
πa
πa 