题目内容
在形如 的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算。
定义:如果 (a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:
(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作: ,例如:求
,例如:求 ,因为
,因为 =8,所以
=8,所以 =3;又比如∵
=3;又比如∵ ,∴
,∴ .
.
小题1:根据定义计算:(本小题6分)
① =____;②
=____;② = ;
= ;
③如果 ,那么x= 。
,那么x= 。
小题2:设 则
则 (a>0,a≠1,M、N均为正数),
(a>0,a≠1,M、N均为正数),
∵ ,∴
,∴ ∴
∴ ,
,
即
这是对数运算的重要性质之一,进一步,我们还可以得出:
 = .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
= .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
小题3:请你猜想: (a>0,a≠1,M、N均为正数).(本小题2分)
(a>0,a≠1,M、N均为正数).(本小题2分)
 的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算。
定义:如果
 (a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:
(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作: ,例如:求
,例如:求 ,因为
,因为 =8,所以
=8,所以 =3;又比如∵
=3;又比如∵ ,∴
,∴ .
.小题1:根据定义计算:(本小题6分)
①
 =____;②
=____;② = ;
= ;③如果
 ,那么x= 。
,那么x= 。小题2:设
 则
则 (a>0,a≠1,M、N均为正数),
(a>0,a≠1,M、N均为正数),∵
 ,∴
,∴ ∴
∴ ,
,即

这是对数运算的重要性质之一,进一步,我们还可以得出:
 = .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
= .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)小题3:请你猜想:
 (a>0,a≠1,M、N均为正数).(本小题2分)
(a>0,a≠1,M、N均为正数).(本小题2分)小题1:因为34=81,所以log381=4;②因为100=1,所以log101=0;③因为24=16,所以x=2.
小题2:logaM1+logaM2+…+logaMn
小题3:logaM-logaN(a>0,a≠1,M、N均为正数)
(1)①因为34=81,所以log381=4;②因为100=1,所以log101=0;③因为24=16,所以x=2.
(2)结合题意的分析,可知logaM1M2M3…Mn=logaM1+logaM2+…+logaMn.
(3)因为logaMN=logaM+logaN,所以可猜想:loga =logaM-logaN(a>0,a≠1,M、N均为正数)
=logaM-logaN(a>0,a≠1,M、N均为正数)
(2)结合题意的分析,可知logaM1M2M3…Mn=logaM1+logaM2+…+logaMn.
(3)因为logaMN=logaM+logaN,所以可猜想:loga
 =logaM-logaN(a>0,a≠1,M、N均为正数)
=logaM-logaN(a>0,a≠1,M、N均为正数)
练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中
从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中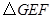 与矩形
与矩形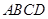 重合部分的面积(S)随时间(t)变化的图象大致是( )
重合部分的面积(S)随时间(t)变化的图象大致是( )




 ,则电子跳蚤连续跳(
,则电子跳蚤连续跳( )步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳
)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳 步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳
步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳 步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为 ;第2012次电子跳蚤能跳到的圆圈内所标的数字为 .
步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为 ;第2012次电子跳蚤能跳到的圆圈内所标的数字为 .

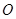 ,以便在里面配置各种应急药物。现要求该取药点离两个广场入口
,以便在里面配置各种应急药物。现要求该取药点离两个广场入口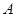 、
、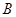 的距离相等,且离观赏点
的距离相等,且离观赏点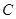 的距离恰好等于
的距离恰好等于