题目内容
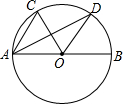 如图,在直径为AB的⊙O中,∠DAB=30°,∠COD=60°,OD∥AC吗,为什么?
如图,在直径为AB的⊙O中,∠DAB=30°,∠COD=60°,OD∥AC吗,为什么?考点:圆周角定理
专题:
分析:由圆周角定理得到∠DOB=60°,则∠AOC=60°,易证△AOC是等边三角形,则∠CAO=60°,由“同位角相等,两直线平行”推知OD∥AC.
解答:解:OD∥AC.理由如下:
∵在直径为AB的⊙O中,∠DAB=30°,
∴∠DOB=2∠DAB=60°,
∵∠COD=60°,
∴∠CAO=60°,
又OA=OC,
∴△AOC是等边三角形,则∠CAO=60°,
∴∠CAO=∠DOB,
∴OD∥AC.
∵在直径为AB的⊙O中,∠DAB=30°,
∴∠DOB=2∠DAB=60°,
∵∠COD=60°,
∴∠CAO=60°,
又OA=OC,
∴△AOC是等边三角形,则∠CAO=60°,
∴∠CAO=∠DOB,
∴OD∥AC.
点评:本题考查了圆周角定理.欲证明OD∥AC,则只需证得同位角或内错角相等即可.

练习册系列答案
相关题目
 美化城市、改善人们的居住环境已成为城市建设的一项重要内容.某区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加,根据图中所提供的信息,下列说法错误的是( )
美化城市、改善人们的居住环境已成为城市建设的一项重要内容.某区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加,根据图中所提供的信息,下列说法错误的是( )| A、2009年该区的绿地面积为420公顷 |
| B、2011年的绿地面积增长最快 |
| C、从2009年到2012年,每年绿地面积的增长率都在增长 |
| D、从2009年到2012年,每年的绿地面积都在增长 |
下列事件中的必然事件是( )
| A、天气阴了之后下雨 |
| B、小明上学路上看到两车相撞 |
| C、抛掷一枚骰子,朝上的一面点数恰好是5 |
| D、同时抛掷两枚骰子,朝上的两面点数之和小于13 |
 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=10,AC=6,则DF的长为
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=10,AC=6,则DF的长为 如图所示,将直角边长为6
如图所示,将直角边长为6 已知二次函数y=x2+bx-1的图象经过点(3,2).
已知二次函数y=x2+bx-1的图象经过点(3,2). 如图,该图中不同的线段数共有
如图,该图中不同的线段数共有