题目内容
如图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是______,第n个叠放的图形中,小正方体木块总数应是______;若露在外面的面都涂上颜色(底面不涂),小正方体的边长为1,则第n个叠放的图形中,涂上颜色的面积是______

解:第n个图形中,从上到下,小正方形的个数为:1+5+9+…+[4(n-1)+1],
=1+5+9+…+(4n-3),
= (1+4n-3)n,
(1+4n-3)n,
=n(2n-1),
当n=7时,7(2×7-1)=91,
从正面看,需涂色的面有:1+3+5+…+(2n-1)=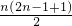 =n2,
=n2,
所以,从前、后、左、右看,需涂色的面有4n2,
从上面看,需涂色的面有:2(2n-1)-1=4n-3,
所以,第n个叠放的图形中,涂上颜色的面有:4n2+4n-3,
面积是4n2+4n-3.
故答案为:91,n(2n-1),4n2+4n-3.
分析:按照从上到下的顺序写出第n个图形中小正方体的个数的表达式,然后计算即可得解;
再把n=7代入表达式进行计算即可得解;
分前后左右四个部分查出涂色的面,从上面分横向与纵向两个方向查出需涂色的面,然后相加,利用求和公式计算即可得解.
点评:本题是对图形变化规律的考查,立体图形比较复杂,注意确定正方体的个数与涂色面数时按照一定的顺序查找方可做到不重不漏,也是解题的关键.
=1+5+9+…+(4n-3),
=
 (1+4n-3)n,
(1+4n-3)n,=n(2n-1),
当n=7时,7(2×7-1)=91,
从正面看,需涂色的面有:1+3+5+…+(2n-1)=
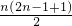 =n2,
=n2,所以,从前、后、左、右看,需涂色的面有4n2,
从上面看,需涂色的面有:2(2n-1)-1=4n-3,
所以,第n个叠放的图形中,涂上颜色的面有:4n2+4n-3,
面积是4n2+4n-3.
故答案为:91,n(2n-1),4n2+4n-3.
分析:按照从上到下的顺序写出第n个图形中小正方体的个数的表达式,然后计算即可得解;
再把n=7代入表达式进行计算即可得解;
分前后左右四个部分查出涂色的面,从上面分横向与纵向两个方向查出需涂色的面,然后相加,利用求和公式计算即可得解.
点评:本题是对图形变化规律的考查,立体图形比较复杂,注意确定正方体的个数与涂色面数时按照一定的顺序查找方可做到不重不漏,也是解题的关键.

练习册系列答案
相关题目




