题目内容
直角三角形的两直角边分别为5厘米,12厘米,其斜边上的高为
- A.6厘米
- B.8.5厘米
- C.
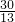 厘米
厘米 - D.
 厘米
厘米
D
分析:本题可先用勾股定理求出斜边长,然后再根据直角三角形面积的两种公式求解即可.
解答:由勾股定理可得:斜边长2=52+122,
则斜边长=13,
直角三角形面积S= ×5×12=
×5×12= ×13×斜边的高,
×13×斜边的高,
可得:斜边的高= .
.
故选D.
点评:本题考查勾股定理及直角三角形面积公式的综合运用,看清题中条件即可.
分析:本题可先用勾股定理求出斜边长,然后再根据直角三角形面积的两种公式求解即可.
解答:由勾股定理可得:斜边长2=52+122,
则斜边长=13,
直角三角形面积S=
 ×5×12=
×5×12= ×13×斜边的高,
×13×斜边的高,可得:斜边的高=
 .
.故选D.
点评:本题考查勾股定理及直角三角形面积公式的综合运用,看清题中条件即可.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 ,
, 表示直角三角形的两直角边(
表示直角三角形的两直角边( ),下列四个说法:
),下列四个说法:
 ,②
,② ,③
,③ ,④
,④ .
.
 ,
, 表示直角三角形的两直角边(
表示直角三角形的两直角边( ),下列四个说法:
),下列四个说法: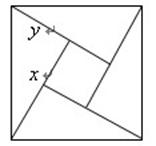
 ,②
,② ,③
,③ ,④
,④ .
.