题目内容
 如图是用四个相同的矩形和一个正方形拼成的图案,已知此图案的总面积是49,小正方形的面积是4,x,y分别表示矩形的长和宽,那么下面式子中不正确的是
如图是用四个相同的矩形和一个正方形拼成的图案,已知此图案的总面积是49,小正方形的面积是4,x,y分别表示矩形的长和宽,那么下面式子中不正确的是
- A.x+y=7
- B.x-y=2
- C.4xy+4=49
- D.x2+y2=25
D
分析:根据大正方形的面积与小正方形的面积的表示,四个矩形的面积的和的两种不同的表示方法列式,然后整理,对各选项分析判断后利用排除法.
解答:A、∵此图案的总面积是49,
∴(x+y)2=49,
∴x+y=7,故本选项正确,不符合题意;
B、∵小正方形的面积是4,
∴(x-y)2=4,
∴x-y=2,故本选项正确,不符合题意;
C、根据题得,四个矩形的面积=4xy,
四个矩形的面积=(x+y)2-(x-y)2=49-4,
∴4xy=49-4,
即4xy+4=49,故本选项正确,不符合题意;
D、∵(x+y)2+(x-y)2=49+4,
∴2(x2+y2)=53,
解得x2+y2=26.5,故本选项错误,符合题意.
故选D.
点评:本题考查了完全平方公式的几何背景,根据同一个图形的面积的不同表示方法列出算式是解题的关键.
分析:根据大正方形的面积与小正方形的面积的表示,四个矩形的面积的和的两种不同的表示方法列式,然后整理,对各选项分析判断后利用排除法.
解答:A、∵此图案的总面积是49,
∴(x+y)2=49,
∴x+y=7,故本选项正确,不符合题意;
B、∵小正方形的面积是4,
∴(x-y)2=4,
∴x-y=2,故本选项正确,不符合题意;
C、根据题得,四个矩形的面积=4xy,
四个矩形的面积=(x+y)2-(x-y)2=49-4,
∴4xy=49-4,
即4xy+4=49,故本选项正确,不符合题意;
D、∵(x+y)2+(x-y)2=49+4,
∴2(x2+y2)=53,
解得x2+y2=26.5,故本选项错误,符合题意.
故选D.
点评:本题考查了完全平方公式的几何背景,根据同一个图形的面积的不同表示方法列出算式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 6、如图是用四个相同的矩形和一个正方形拼成的图案,已知此图案的总面积是49,小正方形的面积是4,x,y分别表示矩形的长和宽,那么下面式子中不正确的是( )
6、如图是用四个相同的矩形和一个正方形拼成的图案,已知此图案的总面积是49,小正方形的面积是4,x,y分别表示矩形的长和宽,那么下面式子中不正确的是( )





 ,宽为
,宽为 的矩形,构造图④
的矩形,构造图④
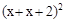 或四个长
或四个长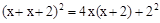




 的解
的解 与
与 的大小关系(其中
的大小关系(其中 )?
)? ,宽
,宽 的矩形,按图⑤方式分割
的矩形,按图⑤方式分割

 ,
, ,即
,即 ,
,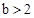 时,表示
时,表示 与
与 的大小关系
的大小关系 ,
,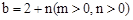 ,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长)
,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长)