题目内容
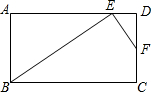
如图，在矩形ABCD中，点E、F分别在边AD、DC上，已知△ABE∽△DEF．
（1）求证：∠BEF=90°；
（2）AB=5，AD=10，DF=2，求AE的长．
（1）求证：∠BEF=90°；
（2）AB=5，AD=10，DF=2，求AE的长．
（1）证明：∵△ABE∽△DEF，
∴∠AEB=∠DFE，
∵∠DFE+∠DEF=90°，
∴∠AEB+∠DEF=90°，
∴∠BEF=90°
（2）∵△ABE∽△DEF，
∴
=
，
∴
=
，
∴AE=5±
．
∴∠AEB=∠DFE，
∵∠DFE+∠DEF=90°，
∴∠AEB+∠DEF=90°，
∴∠BEF=90°
（2）∵△ABE∽△DEF，
∴
| AE |
| DF |
| AB |
| DE |
∴
| AE |
| 2 |
| 5 |
| 10-AE |
∴AE=5±
| 15 |
练习册系列答案
阅读快车系列答案
相关题目
每秒2cm的速度匀速运动，Q在边BC上沿BC方向以每秒1cm的速度匀速运动，当一点到达终点时，另一点也停止运动．设运动时间为x秒，△PBQ的面积为y（cm2）．
