Question

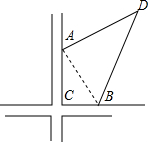如图，李伯伯承包了一块四边形的土地ABCD，他让小亮帮他测量一下这块地的面积．先量得AC的长为120米，BC的长为60米，BD的长为240米．当要测量AD的长度时，小亮说：“不用量了，我已经测得BA恰好平分∠CAB，公路AC和BC是互相垂直的，有了这些条件，就能求出这块土地的面积了．”小亮说得对吗？你会计算这块土地的面积吗？

Answer 1

分析：过点A作AE⊥BD于E，根据角平分线的性质可得AE=AC=120米，从而分别求出△ACB和△ABD的面积，两者相加即可得出这块土地的面积．

解答：解：过点A作AE⊥BD于E，
∵AB正好平分∠CBD，
∴AE=AC=120米，
故可得S_△ACB=

1

2

AC×BC=3600米²，S_△ABD=BD×AE=14400米²，
∴可得这块地的面积=S_△ACB+S_△ABD=18000米²．

点评：此题考查了勾股定理的应用，解答本题的关键是利用角平分线的性质得出AE的长度，然后利用两三角形的面积之和求解答案，难度一般．