题目内容
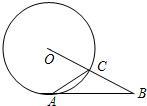
如图，⊙O与AB相切于点A，BO与⊙O交于点C，∠B=26°，则∠OCA=分析：连接OA；根据切线的性质和三角形内角和定理求解．
解答：
解：连接OA．
∵⊙O与AB相切于点A，
∴∠OAB=90°．
∵∠B=26°，
∴∠AOB=180°-∠OAB-∠B=180°-90°-26°=64°．
∵OA=OC，
∴∠1=∠2=
（180°-∠AOB）=
（180°-64°）=58°．
故∠2=58°，即∠OCA=58°．
解：连接OA．∵⊙O与AB相切于点A，
∴∠OAB=90°．
∵∠B=26°，
∴∠AOB=180°-∠OAB-∠B=180°-90°-26°=64°．
∵OA=OC，
∴∠1=∠2=
| 1 |
| 2 |
| 1 |
| 2 |
故∠2=58°，即∠OCA=58°．
点评：此题主要考查切线的性质，三角形的内角和定理及等腰三角形的性质．
练习册系列答案
相关题目
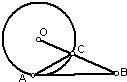9、如图：⊙O与AB相切于点A，BO与⊙O交于点C，∠BAC=24°，则∠B等于
（2012•张家口一模）如图：⊙O与AB相切于点A，BO与⊙O交于点C，∠BAC=30°，则∠B等于（ ）