题目内容
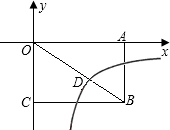 如图,已知矩形OABC的面积为81,它的对角线OB与双曲线
如图,已知矩形OABC的面积为81,它的对角线OB与双曲线 相交于点D,且DB:OD=4:5,则k的值为________.
相交于点D,且DB:OD=4:5,则k的值为________.
-25
分析:过D点作DE⊥OA,设D(m,-n),则OE=m,DE=n,DE∥AB,利用相似三角形对应边成比例,求OA与OB的积,再利用矩形面积公式,列方程求k的值.
解答:如图,过D点作DE⊥OA,垂足为E,
设D(m,-n),则OE=m,DE=n,
∵四边形OABC为矩形,∴DE∥AB,
∴△ODE∽△OBA,∴ =
= =
= =
= ,
,
∴OA= m,AB=
m,AB= n,
n,
∵矩形OABC的面积为81,∴OA•OB=81,即 m×
m× n=81,
n=81,
解得mn=25,
∴k=-mn=-25,
故答案为:-25.
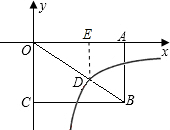
点评:本题考查了反比例函数的综合运用.关键是设D点坐标,表示线段长度,利用相似三角形表示矩形两邻边的积,根据矩形面积公式求两邻边的积.
分析:过D点作DE⊥OA,设D(m,-n),则OE=m,DE=n,DE∥AB,利用相似三角形对应边成比例,求OA与OB的积,再利用矩形面积公式,列方程求k的值.
解答:如图,过D点作DE⊥OA,垂足为E,
设D(m,-n),则OE=m,DE=n,
∵四边形OABC为矩形,∴DE∥AB,
∴△ODE∽△OBA,∴
 =
= =
= =
= ,
,∴OA=
 m,AB=
m,AB= n,
n,∵矩形OABC的面积为81,∴OA•OB=81,即
 m×
m× n=81,
n=81,解得mn=25,
∴k=-mn=-25,
故答案为:-25.

点评:本题考查了反比例函数的综合运用.关键是设D点坐标,表示线段长度,利用相似三角形表示矩形两邻边的积,根据矩形面积公式求两邻边的积.

练习册系列答案
相关题目
 如图,已知:正△OAB的面积为
如图,已知:正△OAB的面积为 长线交于点E.
长线交于点E.


 ,过点D作DE垂直OA的延长线且交于点E.(1)求证:△OAB∽△EDA;
,过点D作DE垂直OA的延长线且交于点E.(1)求证:△OAB∽△EDA;