题目内容
正方形ABCD边长为4,P点在直线BC上,PB=1,将直线AP绕A点逆时针旋转90°后与直线CD交于Q,则CQ=________.
3或5
分析:分①点P在CB的延长线上时,根据正方形的性质可得AB=AD,∠ABC=∠ADC=90°,从而得到∠ABP=∠ADQ,根据旋转的性质可得利用同角的余角相等求出∠PAB=∠QAD,然后利用“角边角”证明△APB和△AQD全等,根据全等三角形对应边相等可得DQ=PB;②点P在线段BC上时,同理求出DQ的长,再根据CQ=CD+DQ计算即可得解.
解答: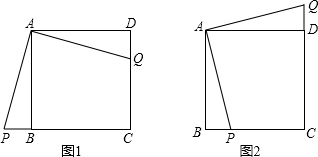 解:①点P在CB的延长线上时,如图1,
解:①点P在CB的延长线上时,如图1,
在正方形ABCD中,AB=AD,∠ABC=∠ADC=90°,
∴∠ABP=∠ADQ=90°,
∵AP绕A点逆时针旋转90°得到AQ,
∴∠PAQ=90°,
∴∠PAB+∠BAQ=90°,
又∵∠DAQ+∠BAQ=∠BAD=90°,
∴∠PAB=∠QAD,
∵在△APB和△AQD中,
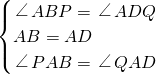 ,
,
∴△APB≌△AQD(ASA),
∴DQ=PB=1,
∴CQ=CD-DQ=4-1=3;
②点P在线段BC上时,如图2,同理求出DQ=PB=1,
∴CQ=CD+DQ=4+1=5,
综上所述,CQ的长是3或5.
故答案为:3或5.
点评:本题考查了正方形的性质,旋转的性质,全等三角形的判定与性质,熟练掌握各性质并求出DQ=PB是解题的关键,难点在于要分情况讨论,作出图形更形象直观.
分析:分①点P在CB的延长线上时,根据正方形的性质可得AB=AD,∠ABC=∠ADC=90°,从而得到∠ABP=∠ADQ,根据旋转的性质可得利用同角的余角相等求出∠PAB=∠QAD,然后利用“角边角”证明△APB和△AQD全等,根据全等三角形对应边相等可得DQ=PB;②点P在线段BC上时,同理求出DQ的长,再根据CQ=CD+DQ计算即可得解.
解答:
 解:①点P在CB的延长线上时,如图1,
解:①点P在CB的延长线上时,如图1,在正方形ABCD中,AB=AD,∠ABC=∠ADC=90°,
∴∠ABP=∠ADQ=90°,
∵AP绕A点逆时针旋转90°得到AQ,
∴∠PAQ=90°,
∴∠PAB+∠BAQ=90°,
又∵∠DAQ+∠BAQ=∠BAD=90°,
∴∠PAB=∠QAD,
∵在△APB和△AQD中,
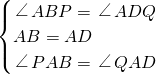 ,
,∴△APB≌△AQD(ASA),
∴DQ=PB=1,
∴CQ=CD-DQ=4-1=3;
②点P在线段BC上时,如图2,同理求出DQ=PB=1,
∴CQ=CD+DQ=4+1=5,
综上所述,CQ的长是3或5.
故答案为:3或5.
点评:本题考查了正方形的性质,旋转的性质,全等三角形的判定与性质,熟练掌握各性质并求出DQ=PB是解题的关键,难点在于要分情况讨论,作出图形更形象直观.

练习册系列答案
相关题目
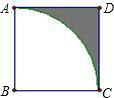 如图,正方形ABCD边长为2cm,以点B为圆心,AB的长为半径作弧
如图,正方形ABCD边长为2cm,以点B为圆心,AB的长为半径作弧 |
| AC |
| A、(4-π)cm2 |
| B、(8-π)cm2 |
| C、(2π-4)cm2 |
| D、(π-2)cm2 |
 正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直. 如图所示,正方形ABCD边长为2,点E在CB的延长线上,BD=BE,则tan∠BAE的值为
如图所示,正方形ABCD边长为2,点E在CB的延长线上,BD=BE,则tan∠BAE的值为 s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.
s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒. 正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,