题目内容
 如图,A(1,2)、B(-1,-2)是函数
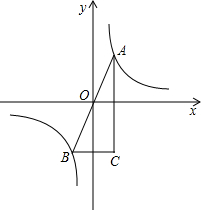
如图,A(1,2)、B(-1,-2)是函数 的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则
的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则
- A.S=2
- B.S=4
- C.S=8
- D.S=1
B
分析:先根据A、B是函数 的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,可知AC⊥x轴,BC⊥y轴,故S△AOD=S△BOE=1,再根据A(1,2)、B(-1,-2)可知OD=1,CD=2,所以S矩形OECD=2,由S=S△AOD+S△BOE+S矩形OECD即可得出结论.
的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,可知AC⊥x轴,BC⊥y轴,故S△AOD=S△BOE=1,再根据A(1,2)、B(-1,-2)可知OD=1,CD=2,所以S矩形OECD=2,由S=S△AOD+S△BOE+S矩形OECD即可得出结论.
解答: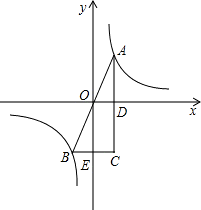 解:∵A、B是函数
解:∵A、B是函数 的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,
的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,
∴AC⊥x轴,BC⊥y轴,四边形OECD是矩形,
∴S△AOD=S△BOE=1,
∵A(1,2)、B(-1,-2),
∴OD=1,CD=2,
∴S矩形OECD=2,
∴S=S△AOD+S△BOE+S矩形OECD=1+1+2=4.
故选B.
点评:本题考查的是反比例函数系数k的几何意义,即在反比例函数y= 的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是 ,且保持不变.
,且保持不变.
分析:先根据A、B是函数
 的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,可知AC⊥x轴,BC⊥y轴,故S△AOD=S△BOE=1,再根据A(1,2)、B(-1,-2)可知OD=1,CD=2,所以S矩形OECD=2,由S=S△AOD+S△BOE+S矩形OECD即可得出结论.
的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,可知AC⊥x轴,BC⊥y轴,故S△AOD=S△BOE=1,再根据A(1,2)、B(-1,-2)可知OD=1,CD=2,所以S矩形OECD=2,由S=S△AOD+S△BOE+S矩形OECD即可得出结论.解答:
 解:∵A、B是函数
解:∵A、B是函数 的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,
的图象上关于原点对称的两点,BC∥x轴,AC∥y轴,∴AC⊥x轴,BC⊥y轴,四边形OECD是矩形,
∴S△AOD=S△BOE=1,
∵A(1,2)、B(-1,-2),
∴OD=1,CD=2,
∴S矩形OECD=2,
∴S=S△AOD+S△BOE+S矩形OECD=1+1+2=4.
故选B.
点评:本题考查的是反比例函数系数k的几何意义,即在反比例函数y=
 的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是 ,且保持不变.
,且保持不变. 
练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.