Question

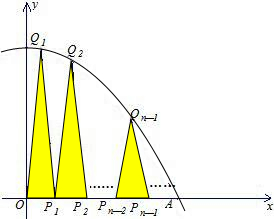
如图，抛物线y=-x²+1与x轴的正半轴交于A点，将OA段的n等分点从左到右分别记为P₁，P₂，…P_n-1，过P_n-1P_n-2的中点分别作x轴的垂线，与抛物线的交点依次记为Q₁，Q₂，…Q_n-1，从而得到n-1个等腰三角形△Q₁OP₁、△Q₂P₁P₂…、△Q_n-1P_n-2P_n-1记这些三角形的面积之和为S，试用n表示为S的函数S_（n）．
提示：1²+2²+3²+…n²=

n(n+1)(2n+1)

6

（n是非零整数）

Answer 1

分析：根据题意可知每个三角形的底边长均为

1

n

，设出OA上第k个分点的坐标P_k，得出第k个三角形底边中点坐标O_k，得出第k个三角形面积的表达式，然后把各个面积加起来即可得到答案．

解答：解：∵OA=1，
∴每个三角形的底边长均为

1

n

，
设OA上的第k个分点为P_k（

k

n

，0）．
记第k个三角形的底边中点为O_k，则O_k为（

2k-1

2n

，0），
代入y=-x²+1中可以得到y=-(

2k-1

2n

)2+1，
∴第k个三角形的面积为fk=

1

2

×

1

n

[-(

2k-1

2n

)2+1]=

1

2n

-

(2k-1)2

8n3

，
∴S=

n-1

2n

-

1

8n3

[12+32+52+…+(2n-3)2]
=

n-1

2n

-

1

8n3

{[12+22+32+…+(2n-3)2+(2n-2)2]-[22+42+…+(2n-2)2]}，
=

n-1

2n

-

1

8n3

{[12+22+32+…+(2n-3)2+(2n-2)2]-22[12+22+32+…+(n-1)2]}
∵12+22+32+••+n2=

n(n+1)(2n+1)

6

，
∴12+22+32+…+(2n-3)2+(2n-2)2=

(2n-2)(2n-1)(4n-3)

6

，
12+22+32+…+(n-1)2=

n(n-1)(2n-1)

6

，
∴S=

n-1

2n

-

1

8n3

{[12+22+32+…+(2n-3)2+(2n-2)2]-22[12+22+…+(n-1)2]}
=

n-1

2n

-

1

8n3

[

(2n-2)(2n-1)(4n-3)

6

-22

n(n-1)(2n-1)

6

]
=

12n3-14n2+5n-3

24n3

．
综上可得S_（n）=

12n3-14n2+5n-3

24n3

．

点评：本题考查了二次函数的运用，要求有很高的计算能力，分式之间的相互转换非常重要，应该记住一些基本的式子．