题目内容
(1)化简:(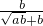 +
+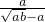 )÷
)÷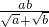 •
•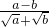
(2)解方程组: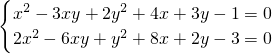 .
.
解:(1)原式=(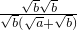 +
+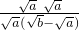 )•
)•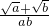 •
•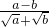 ,
,
=(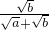 +
+ )•
)• ,
,
=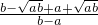 •
• ,
,
=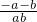 ;
;
(2) ,
,
①×2得:2x2-6xy+4y2+8x+6y-2=0,③
③-②得;3y2+4y+1=0,
解得:y1=-1,y2=- ,
,
把y1=-1代入①得:x2+7x-2=0,
解得:x1=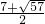 ,x2=
,x2= ,
,
把y2=- 代入①得:x2+5x-
代入①得:x2+5x- =0,
=0,
解得:x1=- ,x2=
,x2= ,
,
∴方程组的解为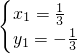 ,
,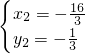 ,
, ,
, .
.
分析:(1)首先把括号里面的分母第一个分子分母约去 ,第二个约去
,第二个约去 ,再把括号里面通分化简,括号外面的变除法为乘法,约分计算即可;
,再把括号里面通分化简,括号外面的变除法为乘法,约分计算即可;
(2)首先把①×2-2可得到一个关于y的一元二次方程,解可得到y的值,再把y的值分别代入①,可得到关于x的一元二次方程,再解出x的值,即可得到答案.
点评:此题主要考查了高次方程,以及分式的化简,①二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰;②解方程组关键是消元思想的运用.
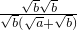 +
+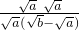 )•
)•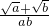 •
•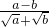 ,
,=(
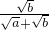 +
+ )•
)• ,
,=
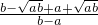 •
• ,
,=
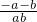 ;
;(2)
 ,
,①×2得:2x2-6xy+4y2+8x+6y-2=0,③
③-②得;3y2+4y+1=0,
解得:y1=-1,y2=-
 ,
,把y1=-1代入①得:x2+7x-2=0,
解得:x1=
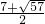 ,x2=
,x2= ,
,把y2=-
 代入①得:x2+5x-
代入①得:x2+5x- =0,
=0,解得:x1=-
 ,x2=
,x2= ,
,∴方程组的解为
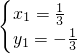 ,
,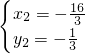 ,
, ,
, .
.分析:(1)首先把括号里面的分母第一个分子分母约去
 ,第二个约去
,第二个约去 ,再把括号里面通分化简,括号外面的变除法为乘法,约分计算即可;
,再把括号里面通分化简,括号外面的变除法为乘法,约分计算即可;(2)首先把①×2-2可得到一个关于y的一元二次方程,解可得到y的值,再把y的值分别代入①,可得到关于x的一元二次方程,再解出x的值,即可得到答案.
点评:此题主要考查了高次方程,以及分式的化简,①二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰;②解方程组关键是消元思想的运用.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
