Question

边长为a的正三角形的内切圆半径是________．

Answer 1

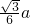
分析：根据等边三角形的三线合一，可以构造一个由其内切圆的半径、外接圆的半径和半边组成的30°的直角三角形，利用锐角三角函数关系求出内切圆半径即可．
解答：解：∵内切圆的半径、外接圆的半径和半边组成一个30°的直角三角形，
则∠OBD=30°，BD=，
∴tan∠BOD==，
∴内切圆半径OD=×=a．
点评：此题主要考查了三角形的内切圆，注意：根据等边三角形的三线合一，可以发现其内切圆的半径、外接圆的半径和半边正好组成了一个30°的直角三角形．