题目内容
已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C．
（1）如图①，若AB=2，∠P=30°，求AP的长（结果保留根号）；
（2）如图②，若D为AP的中点，求证：直线CD是⊙O的切线．
解：（1）∵AB是⊙O的直径，AP是切线，
∴∠BAP=90°．
在Rt△PAB中，AB=2，∠P=30°，
∴BP=2AB=2×2=4．
由勾股定理，得
． （5分）
（2）如图，连接OC、AC．
∵AB是⊙O的直径，
∴∠BCA=90°，又∵∠ACP=180°﹣∠BCA=90°．
在Rt△APC中，D为AP的中点，
∴
．
∴∠4=∠3．
又∵OC=OA，
∴∠1=∠2．
∵∠2+∠4=∠PAB=90°，
∴∠1+∠3=∠2+∠4=90°．
即OC⊥CD．
∴直线CD是⊙O的切线． （8分）
练习册系列答案
一线名师提优试卷系列答案
相关题目
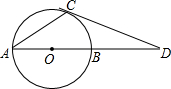如图，已知AB是⊙O的直径，∠CAB=30°，过点C的⊙O的切线交AB延长线于D，若OD=
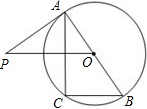如图，已知AB是⊙O的直径，过点O作弦BC的平行线，交过点A的切线AP于点P，连接AC．
如图，已知AB是⊙O的直径，AD切⊙O于点A，