Question

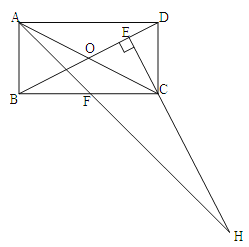
【题目】在四边形ABCD中，对角线相交于点O；E、F、G、H分别是AD、BD、 BC、AC的中点．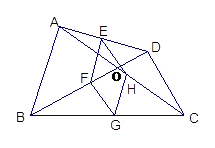

（1）说明四边形EFGH是平行四边形；
（2）当四边形ABCD满足一个什么条件时，四边形EFGH是菱形？并说明理由.

Answer 1

【答案】
（1）解：∵E、F分别是AD，BD的中点，G、H分别中BC，AC的中点，∴EF∥AB， ，GH ∥AB， ，∴EF∥GH， ，∴四边形EFGH是平行四边形
（2）当 时，四边形EFGH是菱形
【解析】（1）三角形的中位线平行于第三边，并且等于第三边的一半。根据这个定理可得EF∥GH， E F = G H ，再由有一组对边平行且相等的四边形是平行四边形可得四边形EFGH是平行四边形。
（2）当AB=CD时，四边形EFGH是菱形。根据中位线定理可知E F =AB，EH=CD，而AB=CD，所以EF=EH，根据有一组邻边相等的平行四边形是菱形可得四边形EFGH是菱形。