题目内容
 如图,△ABC在平面直角坐标系中三个顶点的坐标分别为 A(1,1),B(2,-1),C(3,0)
如图,△ABC在平面直角坐标系中三个顶点的坐标分别为 A(1,1),B(2,-1),C(3,0)(1)作出△ABC关于y轴对称的图形△DEF.
(2)分别写出D、E、F三点的坐标.
(3)求△ABC的面积.
分析:(1)补充成网格结构,然后找出点A、B、C关于y轴的对称点D、E、F的位置,再顺次连接即可;
(2)根据平面直角坐标系写出点D、E、F的坐标即可;
(3)利用△ABC所在的矩形的面积减去四周三个直角三角形的面积,列式进行计算即可得解.
(2)根据平面直角坐标系写出点D、E、F的坐标即可;
(3)利用△ABC所在的矩形的面积减去四周三个直角三角形的面积,列式进行计算即可得解.
解答: 解:(1)如图所示,△DEF即为△ABC关于y轴对称的图形;
解:(1)如图所示,△DEF即为△ABC关于y轴对称的图形;
(2)D(-1,1)、E(-2,-1)、F(-3,0);
(3)△ABC的面积=2×2-
×2×1-
×1×1-
×2×1
=4-1-0.5-1
=4-2.5
=1.5.
 解:(1)如图所示,△DEF即为△ABC关于y轴对称的图形;
解:(1)如图所示,△DEF即为△ABC关于y轴对称的图形;(2)D(-1,1)、E(-2,-1)、F(-3,0);
(3)△ABC的面积=2×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4-1-0.5-1
=4-2.5
=1.5.
点评:本题考查了利用轴对称变换作图,补充成网格结构并准确找出对应点的位置是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
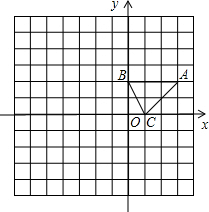 如图,△ABC在平面直角坐标系中,点A(3,2)、B(0,2)、C(1,0).解答问题:
如图,△ABC在平面直角坐标系中,点A(3,2)、B(0,2)、C(1,0).解答问题: 24、如图,△ABC在平面直角坐标系内三顶点坐标分别为A(1,2),B(3,3),C(3,1)
24、如图,△ABC在平面直角坐标系内三顶点坐标分别为A(1,2),B(3,3),C(3,1)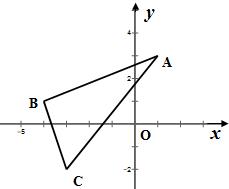 24、如图,△ABC在平面直角坐标系中A(1,3),B(-4,1),C(-3,2),以x轴为对称轴作对称变换,画出△A1B1C1,同时在x轴上找一点P,使P到A、B两点距离和最小?
24、如图,△ABC在平面直角坐标系中A(1,3),B(-4,1),C(-3,2),以x轴为对称轴作对称变换,画出△A1B1C1,同时在x轴上找一点P,使P到A、B两点距离和最小? 如图,△ABC在平面直角坐标系内三顶点坐标分别为A(1,2),B(3,3),C(3,1).
如图,△ABC在平面直角坐标系内三顶点坐标分别为A(1,2),B(3,3),C(3,1). 如图,△ABC在平面直角坐标系中,画出△ABC关于原点的对称图形△A1B1C1,并写出A1、B1、C1的坐标.
如图,△ABC在平面直角坐标系中,画出△ABC关于原点的对称图形△A1B1C1,并写出A1、B1、C1的坐标.