Question

【题目】如图，AB是⊙O的直径，点E为BC的中点，AB=4，∠BED=120°，则图中阴影部分的面积之和为（　　）.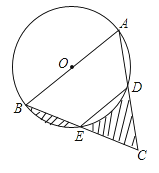

A.
B.2
C.
D.1

Answer 1

【答案】A
【解析】解答: 连接AE，OD、OE．
∵AB是直径，
∴∠AEB=90°，
又∵∠BED=120°，
∴∠AED=30°，
∴∠AOD=2∠AED=60°．
∵OA=OD
∴△AOD是等边三角形，
∴∠OAD=60°，
∵点E为BC的中点，∠AEB=90°，
∴AB=AC，
∴△ABC是等边三角形，边长是4．△EDC是等边三角形，边长是2．
∴∠BOE=∠EOD=60°，
∴ 弧BE和弦BE围成的部分的面积=弧DE和弦DE围成的部分的面积．
∴阴影部分的面积=S△EDC= 故选：A．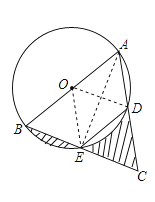

首先证明△ABC是等边三角形．则△EDC是等边三角形，边长是2．而弧BE和弦BE围成的部分的面积=弧DE和弦DE围成的部分的面积．据此即可求解．
【考点精析】认真审题，首先需要了解扇形面积计算公式(在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）)．