题目内容
【题目】如图,已知![]() 、
、![]() ,
,![]() ,
,![]() 为
为![]() 点关于
点关于![]() 的对称点,反比例函数
的对称点,反比例函数![]() 的图像经过
的图像经过![]() 点.
点.

(![]() )证明四边形
)证明四边形![]() 为菱形.
为菱形.
(![]() )求此反比例函数的解析式.
)求此反比例函数的解析式.
(![]() )已知点
)已知点![]() 在
在![]() 的图像上,点
的图像上,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 、
、![]() 、
、![]() 、
、![]() 组成四边形是平行四边形,求
组成四边形是平行四边形,求![]() 点的坐标.
点的坐标.
【答案】(![]() )证明见解析(
)证明见解析(![]() )
)![]() (
(![]() )
)![]() 点的坐标为
点的坐标为![]() ,
,![]() ,
,![]()
【解析】
试题(![]() )先计算出
)先计算出![]() ,
,![]() ,再根据轴对称的性质得
,再根据轴对称的性质得![]() ,
,![]() ,于是可根据菱形的判定方法得到四边形
,于是可根据菱形的判定方法得到四边形![]() 为菱形;
为菱形;
(![]() )由菱形的性质得
)由菱形的性质得![]() ,则
,则![]() ,然后把
,然后把![]() 点坐标代入关系式求出
点坐标代入关系式求出![]() 的值即可得到反比例函数解析式;
的值即可得到反比例函数解析式;
(![]() )讨论:当
)讨论:当![]() 为对角线,利用平行四边形的性质,可把
为对角线,利用平行四边形的性质,可把![]() 点向右平移
点向右平移![]() 个单位可得
个单位可得![]() 点,则
点,则![]() 点向右平移
点向右平移![]() 个单位可得
个单位可得![]() 点,则利用反比例函数解析式可确定
点,则利用反比例函数解析式可确定![]() 坐标,于是得到
坐标,于是得到![]() 点通过平移可得
点通过平移可得![]() 点,利用同样平移得到
点,利用同样平移得到![]() 点坐标,当
点坐标,当![]() 为边,由四边形
为边,由四边形![]() 为平行四边形得到
为平行四边形得到![]() ,
,![]() ,则可确定
,则可确定![]() 坐标,进而可求
坐标,进而可求![]() ,
,![]() 及
及![]() ,易得
,易得![]() 点坐标.
点坐标.
试题解析:(![]() )∵
)∵![]() 、
、![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 为
为![]() 点关于
点关于![]() 的对称点,
的对称点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 为菱形.
为菱形.
(![]() )∵四边形
)∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,
而![]() ,
,![]() ,
,
∴![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
∴反比例函数解析式为![]() .
.
(![]() )当
)当![]() 为对角线,如图,
为对角线,如图,
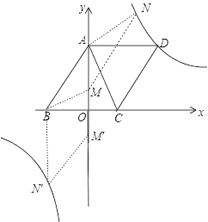
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() 点向右平移
点向右平移![]() 个单位可得
个单位可得![]() 点,
点,![]() 点向右平移
点向右平移![]() 个单位可得
个单位可得![]() 点,
点,
∴![]() 点的横坐标为
点的横坐标为![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
∴![]() 点向右平移
点向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 单位可得
单位可得![]() 点,
点,
∴![]() 点向右平移
点向右平移![]() 个单位可得
个单位可得![]() 点,再向上平移
点,再向上平移![]() 单位可得
单位可得![]() 点,此时
点,此时![]() 点坐标为
点坐标为![]() ;
;
当![]() 为边,
为边,
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,![]() ,
,
∴![]() 点的横坐标为
点的横坐标为![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,或
,或![]() ,
,
此时![]() 点坐标为
点坐标为![]() 或
或![]() ,
,
综上所述,满足条件的![]() 点的坐标为
点的坐标为![]() ,
,![]() ,
,![]() .
.

练习册系列答案
相关题目