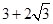题目内容
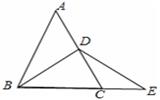
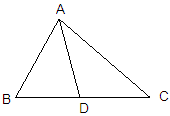
如图：△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E，且AB=6㎝，则△DEB的周长是（ ）
| A．6㎝ | B．4㎝ | C．10㎝ | D．以上都不对 |
A
试题分析：先根据角平分线的性质，结合∠C=90°，DE⊥AB，公共边AD证得△CAD≌△EAD，得到AC=AE，DE=CD，于是BD+DE=BC=AC=AE，即可得到结果．
∵AD平分∠CAB，∠C=90°，DE⊥AB，
∴∠CAD=∠BAD，∠C=∠AED．
∵AD=AD，
∴△CAD≌△EAD，
∴AC=AE，CD=DE．
∵AC=BC，
∴BC=AE．
∴△DEB的周长为DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=6cm，
故选A.
点评：解答本题的关键是利用全等把所求的三角形的周长的各边转移到已知的线段上．
练习册系列答案
名校课堂系列答案
相关题目
