Question

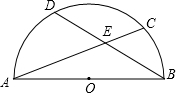如图，设AB为半圆直径，弦AC和BD交于点E，求证：AB²=AE•AC+BE•BD．

Answer 1

证明：连接BC，AD，
根据直径所对的圆周角是直角，得∠C=∠D=90°，
根据相交弦定理，得AE•CE=DE•EB
∴AE•AC+BE•BD=AC²-AC•CE+BD²-BD•DE
=AB²-BC²+AB²-AD²-AC•CE-BD•DE
=2AB²-BE²+CE²-AE²+DE²-AC•CE-BD•DE
=2AB²-AE•AC-BE•BD，
∴AE•AC+BE•BD=AB²．
分析：连接AD、BC构造出两个直角，再利用相交弦定理和勾股定理列式后，进行整式变形即可求解．
点评：本题考查了圆周角定理及相似三角形的判定与性质，此题要熟练运用相交弦定理、勾股定理以及整式的变形整理．