题目内容
(本题8分)如图,已知点P是反比例函数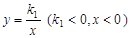 图像上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数
图像上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交反比例函数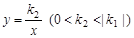 图像于E、F两点.
图像于E、F两点.
(1) 用含k1、k2的式子表示以下图形面积:
① 四边形PAOB;② 三角形OFB;③ 四边形PEOF;
(2) 若P点坐标为(-4,3),且PB︰BF=2︰1,分别求出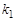 、
、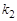 的值.
的值.

【答案】
(1)① S 四边形PAOB=|k1|② S三角形OFB= ③ S四边形PEOF=
③ S四边形PEOF= (或
(或 )(2)
)(2) =-12,
=-12, =6
=6
【解析】
试题分析:(1)① S 四边形PAOB=|k1| ------------1分
② S三角形OFB= ------------1分
------------1分
③ S四边形PEOF= (或
(或 )------------2分
)------------2分
(2)因为P(-4,3)在 上,∴
上,∴ =-12------------2分
=-12------------2分
又PB︰BF=2︰1,∴F(2,3), =6
-------------------2分
=6
-------------------2分
考点:本题考查了反比例函数的性质
点评:此类试题属于难度一般的试题,考生在解答此类试题时一定要对反比例函数的基本性质以及和其它函数的关系牢牢把握

练习册系列答案
相关题目
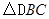 中,
中,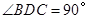 ,
, 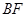 平分
平分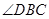 ,与
,与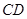 相交于点
相交于点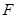 ,延长
,延长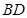 到
到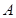 ,使
,使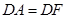 ,
,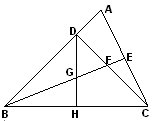
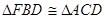 ;
;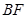 交
交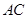 于
于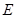 ,且
,且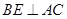 ,)试说明:
,)试说明: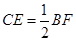 ;
;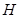 是
是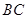 边的中点,连结
边的中点,连结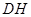 与
与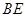 相交于点
相交于点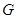 .
. ,
,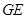 ,
,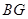 之间的数量关系,并说明理由
之间的数量关系,并说明理由
 .
.
 ,求
,求 的值和这个一次函数的解析式;
的值和这个一次函数的解析式; 轴、
轴、 轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
轴分别交于C、D,求过A、B、D三点的二次函数的解析式; 的面积
的面积 与
与 的面积S满足:
的面积S满足: ?若存在,求点E的坐标;若不存在,请说明理由.
?若存在,求点E的坐标;若不存在,请说明理由.