题目内容
如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;…;当AB=n时,△AME的面积记为Sn.当n≥2时,Sn﹣Sn﹣1= .

考点:
整式的混合运算。
专题:
规律型。
分析:
根据题意得出图象,根据当AB=n时,BC=1,得出Sn=S矩形ACQN﹣S△ACE﹣S△MQE﹣S△ANM,得出S与n的关系,进而得出当AB=n﹣1时,BC=2,Sn﹣1=![]() n2﹣n+
n2﹣n+![]() ,即可得出
,即可得出
Sn﹣Sn﹣1的值.
解答:
解:如图所示:延长CE与NM,交于点Q,
∵线段AC=n+1(其中n为正整数),
∴当AB=n时,BC=1,
∴当△AME的面积记为:
Sn=S矩形ACQN﹣S△ACE﹣S△MQE﹣S△ANM,
=n(n+1)﹣![]() ×1×(n+1)﹣
×1×(n+1)﹣![]() ×1×(n﹣1)﹣
×1×(n﹣1)﹣![]() ×n×n,
×n×n,
=![]() n2,
n2,
当AB=n﹣1时,BC=2,
∴当△AME的面积记为:
Sn﹣1=S矩形ACQN﹣S△ACE﹣S△MQE﹣S△ANM,
=(n+1)(n﹣1)﹣![]() ×2×(n+1)﹣
×2×(n+1)﹣![]() ×2×(n﹣3)﹣
×2×(n﹣3)﹣![]() ×(n﹣1)(n﹣1),
×(n﹣1)(n﹣1),
=![]() n2﹣n+
n2﹣n+![]() ,
,
∴当n≥2时,Sn﹣Sn﹣1=![]() n2﹣(
n2﹣(![]() n2﹣n+
n2﹣n+![]() )=n﹣
)=n﹣![]() =
=![]() ,
,
故答案为:![]() .
.

点评:
此题主要考查了三角形面积求法以及正方形的性质,根据已知得出正确图形,得出S与n的关系是解题关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

 (2011•安宁市一模)下列语句叙述错误的个数是( )
(2011•安宁市一模)下列语句叙述错误的个数是( )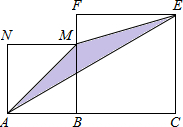 AME的面积记为Sn.当n≥2时,Sn-Sn-1=
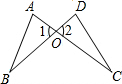
AME的面积记为Sn.当n≥2时,Sn-Sn-1= 如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O中心对称.求证:BF=DE.
如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O中心对称.求证:BF=DE.