题目内容
如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论正确的个数是( )

①AD⊥BC;②∠EDA=∠B;③OA= AC;④DE是⊙O的切线。
AC;④DE是⊙O的切线。
A.1个 B.2个 C.3个 D.4个
D
【解析】
试题分析:根据圆周角定理和切线的判定,采用排除法,逐条分析判断.
【解析】
∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC,故①正确;
连接DO,
∵点D是BC的中点,
∴CD=BD,
∴△ACD≌△ABD(SAS),
∴AC=AB,∠C=∠B,
∵OD=OB,
∴∠B=∠ODB,
∴∠ODB=∠C,OD∥AC,
∴∠ODE=∠CED,
∴ED是圆O的切线,故④正确;
由弦切角定理知,∠EDA=∠B,故②正确;
∵点O是AB的中点,故③正确,
故选D.
考点:切线的判定;全等三角形的判定与性质;圆周角定理;弦切角定理.

练习册系列答案
相关题目

 ,则a是负数;
,则a是负数; 的系数与次数分别为-4和4;
的系数与次数分别为-4和4; 和
和 是同类项,则2m-3n=1;
是同类项,则2m-3n=1;


 有两个不相等的实数根,则a的取值
有两个不相等的实数根,则a的取值 ,
, ,
, 的值;(结果用x、y表示)
的值;(结果用x、y表示) 与
与 互为相反数时,求(1)中代数式的值.
互为相反数时,求(1)中代数式的值. 、
、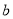 在数轴上的位置如图所示,则下列正确的是( )
在数轴上的位置如图所示,则下列正确的是( )
 B.
B. C.
C. D.
D.
