题目内容
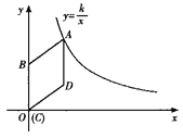
【题目】如图,过反比例函数y=![]() (x>0)的图象上一点A作x轴的平行线,交双曲线y=-
(x>0)的图象上一点A作x轴的平行线,交双曲线y=-![]() (x<0)于点B,过B作BC∥OA交双曲线y=-
(x<0)于点B,过B作BC∥OA交双曲线y=-![]() (x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.
(x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.

【答案】![]()
【解析】
先连接OB,根据比例系数k的几何意义,求得OF=3,由此得到A(2,3),B(-1,3),再求得直线OA的解析式为y=![]() x,直线BC为y=
x,直线BC为y=![]() x+
x+![]() ,再根据解方程组可得D(-2,
,再根据解方程组可得D(-2,![]() ),最后运用待定系数法求得AD解析式为y=
),最后运用待定系数法求得AD解析式为y=![]() x+
x+![]() ,进而得到点E的坐标即可.
,进而得到点E的坐标即可.
如图所示,连接OB,
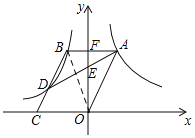
则△AOB的面积=![]() ×|-3|+
×|-3|+![]() ×|6|=
×|6|=![]() ,
,
由AB∥CO,AO∥BC,可得四边形ABCO是平行四边形,
∴AB=CO=3,
∴由![]() ×AB×OF=
×AB×OF=![]() ,可得OF=3,
,可得OF=3,
在y=![]() (x>0)中,令y=3,可得x=2,即A(2,3),
(x>0)中,令y=3,可得x=2,即A(2,3),
在y=-![]() (x<0)中,令y=3,可得x=-1,即B(-1,3),
(x<0)中,令y=3,可得x=-1,即B(-1,3),
由A(2,3)可得,直线OA的解析式为y=![]() x,
x,
可设直线BC为y=![]() x+b,则将B(-1,3)代入可得
x+b,则将B(-1,3)代入可得
3=-![]() +b,解得b=
+b,解得b=![]() ,
,
故BC为y=![]() x+
x+![]() ,
,
解方程组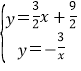 ,可得D(-2,
,可得D(-2,![]() ),
),
设直线AD解析式为y=mx+n,则
将D(-2,![]() ),A(2,3)代入可得
),A(2,3)代入可得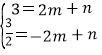 ,
,
解得![]() ,
,
∴AD解析式为y=![]() x+
x+![]() ,
,
令x=0,则y=![]() ,即E(0,
,即E(0,![]() ),
),
∴OE的长为![]() .
.

练习册系列答案
相关题目