题目内容
如图1,抛物线 经过A(-1,0),C(3,-2)两点,与
经过A(-1,0),C(3,-2)两点,与 轴交于点D,与
轴交于点D,与 轴交于另一点B.
轴交于另一点B.
(1)求此抛物线的解析式;
(2)若直线 (
( )将四边形ABCD面积二等分,求
)将四边形ABCD面积二等分,求 的值;
的值;
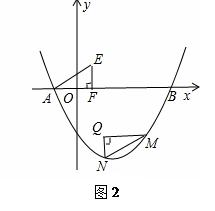
(3)如图2,过点E(1,1)作EF⊥ 轴于点F,将△AEF绕平面内某点P旋转180°得△MNQ(点M、N、Q分别与点A、E、F对应),使点M、N在抛物线上,求点N和点P的坐标?
轴于点F,将△AEF绕平面内某点P旋转180°得△MNQ(点M、N、Q分别与点A、E、F对应),使点M、N在抛物线上,求点N和点P的坐标?
(1)  ;(2)
;(2)  ;(3) (1,-3),(1,-1).
;(3) (1,-3),(1,-1).
解析试题分析:把A、C两点坐标代入 即可求出a、b的值,从而确定抛物线的解析式.
即可求出a、b的值,从而确定抛物线的解析式.
(1)∵抛物线 经过A(-1,0),C(3,-2),
经过A(-1,0),C(3,-2),
∴ ,解之得:
,解之得: ,
,
∴所求抛物线的解析式为: ;
;
(2)令 ,解得:x1=-1,x2=4,
,解得:x1=-1,x2=4,
∴B(4,0),
令x=0,可得:y=-2,
∴D(0,-2),
∵C(3,-2),
∴DC∥AB,
由勾股定理得:AD=BC= ,
,
∴四边形ADCB是等腰梯形,
∵D(0,-2),C(3,-2),∴取DC中点E,则E的坐标是( ,-2),
,-2),
过E作EF⊥AB于F,取EF的中点G,则G的坐标是( ,-1),
,-1),
则过G的直线(直线与AB和CD相交)都能把等腰梯形ABCD的面积二等份,
把G的坐标代入y=kx+1,得: ,
,
∴ ;
; 
(3)设Q(m,n),则M(m+2,n),N(m,n-1),
代入 ,得:
,得: ,解之,得:
,解之,得: ,
,
∴Q(1,-2),M(3,-2),N(1,-3),
又Q的对应点为F(1,0),
∴QF的中点为旋转中心P,且P(1,-1),
∴点N、P的坐标分别为:(1,-3),(1,-1).
考点:二次函数综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,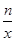 (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;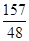 ,试求出t的取值范围.
,试求出t的取值范围. 经过点A(3,2),B(0,1)和点C
经过点A(3,2),B(0,1)和点C .
. ,求点F的坐标;
,求点F的坐标;


 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S. 时,求S的值.
时,求S的值. 的函数解析式.
的函数解析式. 时,求
时,求 的值;
的值; ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.
 (m是常数)
(m是常数)
