题目内容
 如图,小明为了测量一铁塔的高度CD,他先在A处测得塔顶C的仰角为30°,再向塔的方向直行40米到达B处,又测得塔顶C的仰角为60°,请你帮助小明计算出这座铁塔的高度.(小明的身高忽略不计,结果精确到0.1米,参考数据:
如图,小明为了测量一铁塔的高度CD,他先在A处测得塔顶C的仰角为30°,再向塔的方向直行40米到达B处,又测得塔顶C的仰角为60°,请你帮助小明计算出这座铁塔的高度.(小明的身高忽略不计,结果精确到0.1米,参考数据:| 2 |
| 3 |
| 5 |
分析:先根据三角形外角的性质得出∠ACB=30°,进而得出AB=BC=40,在Rt△BDC中,sin60°=
即可求出CD的长.
| CD |
| BC |
解答: 解:∵∠CBD=60°,∠CAB=30°,
解:∵∠CBD=60°,∠CAB=30°,
∴∠ACB=30°.
∴AB=BC=40.(2分)
在Rt△BDC中,sin60°=
∴CD=BC•sin60°=40×
=20
≈34.6(米).(5分)
答:这座铁塔的高度是34.6米.
 解:∵∠CBD=60°,∠CAB=30°,
解:∵∠CBD=60°,∠CAB=30°,∴∠ACB=30°.
∴AB=BC=40.(2分)
在Rt△BDC中,sin60°=
| CD |
| BC |
∴CD=BC•sin60°=40×
| ||
| 2 |
| 3 |
答:这座铁塔的高度是34.6米.
点评:本题考查的是解直角三角形的应用-仰角俯角问题,此题涉及到三角形外角的性质、锐角三角函数的定义及特殊角的三角函数值,熟知以上知识是解答此题的关键.

练习册系列答案
相关题目
 ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.24)
≈2.24)
 ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.24)
≈2.24)
 如图,小明为了测量一铁塔的高度CD,他先在A处测得塔顶C的仰角为30°,再向塔的方向直行40米到达B处,又测得塔顶C的仰角为60°,请你帮助小明计算出这座铁塔的高度.(小明的身高忽略不计,结果精确到0.1米,参考数据:
如图,小明为了测量一铁塔的高度CD,他先在A处测得塔顶C的仰角为30°,再向塔的方向直行40米到达B处,又测得塔顶C的仰角为60°,请你帮助小明计算出这座铁塔的高度.(小明的身高忽略不计,结果精确到0.1米,参考数据: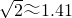 ,
,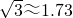 ,
, )
) ,
, ,
, )
)