Question

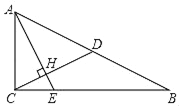
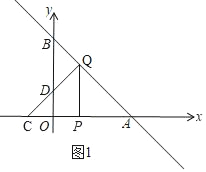
【题目】如图1，直线AB与x轴、y轴分别交于点A（3，0）、B，动点P从原点出发，以每秒1个单位长度的速度向点A运动，到达点A立即停止．点C（﹣1，0），以P为直角顶点，PC为直角边向x轴上方作等腰Rt△PQC，△PQC与△AOB重叠部分面积为S，点P运动时间为t（秒），S关于t的函数图象如图2所示（其中0≤t≤,≤t≤3时，函数解析式不同）．

（1）当t＝时，S的值为　 　；

（2）求直线AB的解析式；

（3）求S关于t的解析式，并写出t的取值范围．

Answer 1

【答案】（1）；（2）y＝﹣x+4；（3）．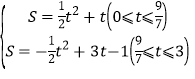

【解析】

（1）由图2可知：当t＝时，Q在AB上，画图1，根据面积差可得结论；

（2）先根据平行相似计算OB的长，得点B的坐标，利用待定系数法可得结论；

（3）分两种情况：0≤t≤，≤t≤3时，分别根据面积差可得对应解析式．

解：（1）当Q在AB上时，如图1，

由题意得：OP＝，OC＝1，

∴PC＝PQ＝1+＝，

∵△PQC和△COD都是等腰直角三角形，

∴S＝S△PCQ﹣S△COD＝ ﹣ 11＝，

故答案为：；

（2）∵A（3，0），

∴OA＝3，

∴AP＝3﹣＝，

∵PQ∥OB，

∴△AQP∽△ABO，

∴，

∴，OB＝4，

∴B（0，4），

设直线AB的解析式为：y＝kx+b，

把A（3，0）、B（0，4）代入得：，

解得：，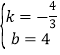

∴直线AB的解析式为：y＝﹣x+4；

（3）由题意得：OP＝t，

当0≤t≤时，如图2，

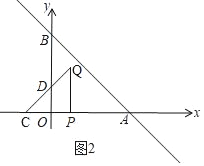
△PQC与△AOB重叠部分是梯形ODQP，

S＝S△PCQ﹣S△COD＝(t+1)2-×1×1=t2+t；

当≤t≤3时，如图3，

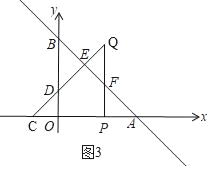
△PQC与△AOB重叠部分是五边形ODEFP，

∵OP＝t，AP＝PF＝3﹣t，

∴FQ＝t+1﹣（3﹣t）＝2t﹣2，

∵∠Q＝∠EFQ＝∠AFP＝45°，

∴∠FEQ＝90°，

∴EQ＝EF＝，

S＝S△PCQ﹣S△COD﹣S△EFQ＝t2+t﹣＝﹣+3t﹣1；

综上，S关于t的解析式为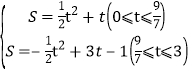：．