题目内容
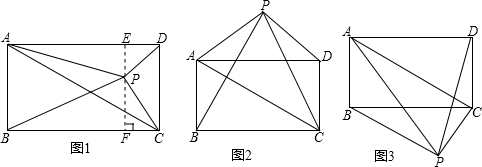
已知矩形ABCD和点P，当点P在图1中的位置时，则有结论：S△PBC=S△PAC+S△PCD
理由：过点P作EF垂直BC，分别交AD、BC于E、F两点．
∵S△PBC+S△PAD=
BC•PF+AD•PE=BC（PF+PE）=BC•EF=S矩形ABCD，
又∵S△PAC+S△PCD+S△PAD=S矩形ABCD，∴S△PBC+S△PAD=S△PAC+S△PCD+S△PAD，∴S△PBC=S△PAC+S△PCD．
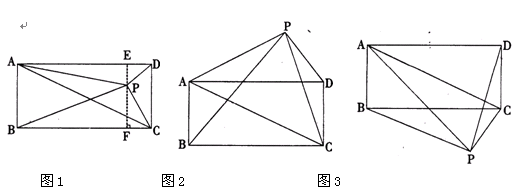
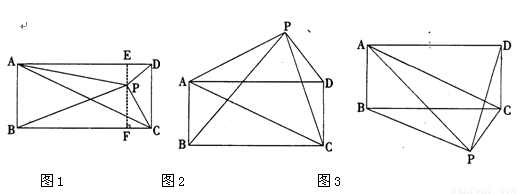
请你参考上述信息，当点P分别在图2，图3中的位置时，S△PBC、S△PAC、S△PCD又有怎样的数量关系？请写出你对上述两种情况的猜想，并选择其中一种情况的猜想给予证明．
解：猜想结果：图2结论S△PBC=S△PAC+S△PCD
图3结论S△PBC=S△PAC-S△PCD
证明：如图2，过点P作EF垂直AD，分别交AD、BC于E、F两点，
∵S△PBC=BC•PE+BC•EF
=AD•PE+BC•EF=S△PAD+S矩形ABCD
∵S△PAC+S△PCD=S△PAD+S△ADC=S△PAD+S矩形ABCD
∴S△PBC=S△PAC+S△PCD
如果证明图3结论可参考上面评分标准给分．
分析：分析图2，先过点P作EF垂直AD，分别交AD、BC于E、F两点，利用三角形的面积公式可知，经过化简，等量代换，可以得到S△PBC=S△PAD+S矩形ABCD，而S△PAC+S△PCD=S△PAD+S矩形ABCD，故有S△PBC=S△PAC+S△PCD．
点评：本题利用了三角形的面积公式，以及图形面积的整合等知识．
图3结论S△PBC=S△PAC-S△PCD
证明：如图2，过点P作EF垂直AD，分别交AD、BC于E、F两点，
∵S△PBC=
BC•PE+BC•EF =
AD•PE+BC•EF=S△PAD+S矩形ABCD∵S△PAC+S△PCD=S△PAD+S△ADC=S△PAD+
S矩形ABCD∴S△PBC=S△PAC+S△PCD
如果证明图3结论可参考上面评分标准给分．
分析：分析图2，先过点P作EF垂直AD，分别交AD、BC于E、F两点，利用三角形的面积公式可知，经过化简，等量代换，可以得到S△PBC=S△PAD+
S矩形ABCD，而S△PAC+S△PCD=S△PAD+S矩形ABCD，故有S△PBC=S△PAC+S△PCD．点评：本题利用了三角形的面积公式，以及图形面积的整合等知识．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
