Question

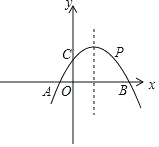
【题目】如图，已知抛物线y＝ax2+bx+1与x轴分别交于A(﹣1，0)，B(3，0)，与y轴交于点C．

(1)求抛物线解析式；

(2)在直线BC上方的抛物线上有点P，使△PBC面积为1，求出点P的坐标．

Answer 1

【答案】(1)y＝﹣x2+x+1；(2)点P的坐标为(1，)或(2，1)．

【解析】

（1）根据抛物线y=ax2+bx+1与x轴分别交于A（-1，0），B（3，0），可以求得该抛物线的解析式；

（2）根据题意和（1）中的抛物线解析式可以求得点C的坐标，从而可以得到直线BC的函数解析式，然后根据在直线BC上方的抛物线上有点P，使△PBC面积为1，即可求得点P的坐标．

（1）∵抛物线y=ax2+bx+1与x轴分别交于A（-1，0），B（3，0），

∴，解得，，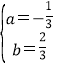

∴抛物线的解析式为y=-x2+x+1；

（2）∵y=-x2+x+1，

∴当x=0时，y=1，

即点C的坐标为（0，1），

∵B（3，0），C（0，1），

∴直线BC的解析式为：y=x+1，

设点P的坐标为（p，-p2+p+1），

将x=p代入y=x+1得y=p+1，

∵△PBC面积为1，

∴，

解得，p1=1，p2=2，

当p1=1时，点P的坐标为（1，），

当p2=2时，点P的坐标为（2，1），

即点P的坐标为（1，）或（2，1）．