题目内容
解方程组
解:由(2)得:(x-2y+2)(x-2y-4)=0
∴原方程组可化为 和
和 .
.
把(3)化为x=2y-2,
代入(1)得:8y(y-1)=0,
∴y=0或y=1,
代入(1)得: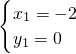 ,
, ;
;
把(4)变形为x=4+2y代入(1)得,8y2+16y+12=0,
△=162-4×8×12=-128<0,故方程无解.
∴原方程组的解是: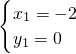 ,
, .
.
分析:(2)可化为:(x-2y+2)(x-2y-4)=0,再转化为两个方程组后,再用代入法求解.
点评:此题比较复杂,解答此题的关键是把原方程组化为两个方程组,再根据判别式求解.
∴原方程组可化为
 和
和 .
.把(3)化为x=2y-2,
代入(1)得:8y(y-1)=0,
∴y=0或y=1,
代入(1)得:
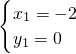 ,
, ;
;把(4)变形为x=4+2y代入(1)得,8y2+16y+12=0,
△=162-4×8×12=-128<0,故方程无解.
∴原方程组的解是:
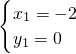 ,
, .
.分析:(2)可化为:(x-2y+2)(x-2y-4)=0,再转化为两个方程组后,再用代入法求解.
点评:此题比较复杂,解答此题的关键是把原方程组化为两个方程组,再根据判别式求解.

练习册系列答案
相关题目
 (1)解方程组:
(1)解方程组: