题目内容
(2009•井研县一模)如图,已知:A(m,2)是一次函数y=kx+b与反比例函数y= 的交点
的交点(1)求m的值;
(2)若该一次函数分别与x轴y轴交于E、F两点,且直角△EOF的外心为点A.试求它的解析式;
(3)在
 的图象上另取一点B,作BK⊥x轴于K,将(2)中的一次函数图象绕点A旋转后所得的直线记为l,若l与y轴的正半轴交于点C,且4CO=FO.试问:在y轴上是否存在点P,使得两个三角形的面积S△PCA=S△BOK?若存在,求点P的坐标,若不存在,请说明理由.
的图象上另取一点B,作BK⊥x轴于K,将(2)中的一次函数图象绕点A旋转后所得的直线记为l,若l与y轴的正半轴交于点C,且4CO=FO.试问:在y轴上是否存在点P,使得两个三角形的面积S△PCA=S△BOK?若存在,求点P的坐标,若不存在,请说明理由.
【答案】分析:(1)根据反比例函数的解析式求得m的值;
(2)根据直角三角形的外心是直角三角形的斜边的中点,由点A的坐标根据三角形的中位线定理可以求得点E,F的坐标,从而求得直线的解析式;
(3)根据反比例函数的解析式,得△BOK的面积是 .再根据点A的横坐标,知PC的长应是2.根据题意可以首先求得点C的坐标,再根据点P可能在点C的上方或下方进行分析.
.再根据点A的横坐标,知PC的长应是2.根据题意可以首先求得点C的坐标,再根据点P可能在点C的上方或下方进行分析.
解答:解:(1)把点A(m,2)代入反比例函数y= 中,得
中,得 (2分)
(2分)
(2)根据直角三角形的外心是直角三角形的斜边的中点,则点A是EF的中点.又A( ,2),
,2),
∴E(3,0),F(0,4)
把E,F代入,得 .解得
.解得
∴ (3分)
(3分)
(3)原直线绕点A旋转所得直线交y轴的正半轴于C,且
得C(0,1)
∵B(xB,yB)在y= 上,则有xB•yB=3,
上,则有xB•yB=3,
由题意有 (4分)
(4分)
设y轴上点P(0,yP),满足S△PCA=S△BOK
①若点P在点C上方,即y>1,有
∴y=3,此时P(0,3)(3分);
②若点P在点C下方,即y<1,有
∴y=-1,此时P(0,-1)(2分).
点评:能够根据函数的解析式求得点的坐标,能够根据点的坐标求得函数的解析式;掌握直角三角形的外心的位置;平行于x轴的线段的长等于两个点的横坐标的差的绝对值,平行于y轴的线段的长度等于两个点的纵坐标的差的绝对值.
(2)根据直角三角形的外心是直角三角形的斜边的中点,由点A的坐标根据三角形的中位线定理可以求得点E,F的坐标,从而求得直线的解析式;
(3)根据反比例函数的解析式,得△BOK的面积是
 .再根据点A的横坐标,知PC的长应是2.根据题意可以首先求得点C的坐标,再根据点P可能在点C的上方或下方进行分析.
.再根据点A的横坐标,知PC的长应是2.根据题意可以首先求得点C的坐标,再根据点P可能在点C的上方或下方进行分析.解答:解:(1)把点A(m,2)代入反比例函数y=
 中,得
中,得 (2分)
(2分)(2)根据直角三角形的外心是直角三角形的斜边的中点,则点A是EF的中点.又A(
 ,2),
,2),∴E(3,0),F(0,4)
把E,F代入,得
 .解得
.解得
∴
 (3分)
(3分)(3)原直线绕点A旋转所得直线交y轴的正半轴于C,且

得C(0,1)
∵B(xB,yB)在y=
 上,则有xB•yB=3,
上,则有xB•yB=3,由题意有
 (4分)
(4分)设y轴上点P(0,yP),满足S△PCA=S△BOK
①若点P在点C上方,即y>1,有

∴y=3,此时P(0,3)(3分);
②若点P在点C下方,即y<1,有

∴y=-1,此时P(0,-1)(2分).
点评:能够根据函数的解析式求得点的坐标,能够根据点的坐标求得函数的解析式;掌握直角三角形的外心的位置;平行于x轴的线段的长等于两个点的横坐标的差的绝对值,平行于y轴的线段的长度等于两个点的纵坐标的差的绝对值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的交点
的交点 的图象上另取一点B,作BK⊥x轴于K,将(2)中的一次函数图象绕点A旋转后所得的直线记为l,若l与y轴的正半轴交于点C,且4CO=FO.试问:在y轴上是否存在点P,使得两个三角形的面积S△PCA=S△BOK?若存在,求点P的坐标,若不存在,请说明理由.
的图象上另取一点B,作BK⊥x轴于K,将(2)中的一次函数图象绕点A旋转后所得的直线记为l,若l与y轴的正半轴交于点C,且4CO=FO.试问:在y轴上是否存在点P,使得两个三角形的面积S△PCA=S△BOK?若存在,求点P的坐标,若不存在,请说明理由.
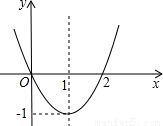
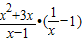 化简,然后请自选你喜欢的一个适合的x值代入,再求原式的值.
化简,然后请自选你喜欢的一个适合的x值代入,再求原式的值.