题目内容
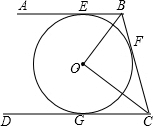
如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD,连接OB、OC,延长CO交⊙O于点M,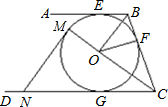 过点M作MN∥OB交CD于N,OB=6cm,OC=8cm.
过点M作MN∥OB交CD于N,OB=6cm,OC=8cm.(1)求∠BOC的度数及⊙O的半径.
(2)请证明MN是⊙O的切线,并求MN的长.
分析:(1)根据切线的性质得到OB平分∠EBF,OC平分∠GCF,OF⊥BC,再根据平行线的性质得∠GCF+∠EBF=180°,则有∠OBF+∠OCF=90°,即∠BOC=90°,然后利用勾股定理计算出BC,再利用等积法计算出OF;
(2)由MN∥OB,而OB⊥OC,得到MN⊥OM,根据切线的判定即可得到MN为⊙O的切线;易证Rt△CMN和Rt△COB相似,利用相似比即可计算出MN的长.
(2)由MN∥OB,而OB⊥OC,得到MN⊥OM,根据切线的判定即可得到MN为⊙O的切线;易证Rt△CMN和Rt△COB相似,利用相似比即可计算出MN的长.
解答:解:(1)∵AB、BC、CD分别与⊙O切于E、F、G,
∴OB平分∠EBF,OC平分∠GCF,OF⊥BC,
又∵AB∥CD,
∴∠GCF+∠EBF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,
在Rt△BOC中,OB=6,OC=8,
∴BC=
=
=10,
又∵
OF•BC=
OB•OC,
∴OF=
=
=4.8(cm);
(2)证明:如图,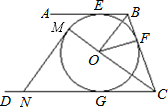
∵MN∥OB,OB⊥OC,
∴MN⊥OM,
∴MN为⊙O的切线,
又∵∠MCN=∠OCB,
∴Rt△CMN∽Rt△COB相似,
∴CM:OC=MN:OB,即(4.8+8):8=MN:6,
∴MN=9.6(cm).
∴OB平分∠EBF,OC平分∠GCF,OF⊥BC,
又∵AB∥CD,
∴∠GCF+∠EBF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,
在Rt△BOC中,OB=6,OC=8,
∴BC=
| OB2+OC2 |
| 62+82 |
又∵
| 1 |
| 2 |
| 1 |
| 2 |
∴OF=
| OB•OC |
| BC |
| 6×8 |
| 10 |
(2)证明:如图,

∵MN∥OB,OB⊥OC,
∴MN⊥OM,
∴MN为⊙O的切线,
又∵∠MCN=∠OCB,
∴Rt△CMN∽Rt△COB相似,
∴CM:OC=MN:OB,即(4.8+8):8=MN:6,
∴MN=9.6(cm).
点评:本题考查了切线的判定与性质定理:过半径的外端点与半径垂直的直线为圆的切线;圆的切线垂直于过切点的半径;过圆外一点引圆的两条切线,切线长相等,圆心与这点的连线平分两切线的夹角.也考查了勾股定理以及相似三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB,BC是⊙O的两条弦,AB垂直平分半径OD,∠ABC=75°,BC=
如图,AB,BC是⊙O的两条弦,AB垂直平分半径OD,∠ABC=75°,BC= 如图,AB,BC分别是⊙O的直径和弦,点D为
如图,AB,BC分别是⊙O的直径和弦,点D为
 如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,BO=6cm,CO=8cm.求BC的长.
如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,BO=6cm,CO=8cm.求BC的长.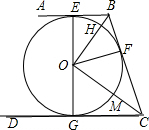 如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.
如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.