题目内容
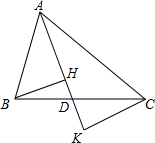 如图,AD是△ABC的角平分线,BH⊥AD,CK⊥AD,垂足分别为点H、K,你能说明AB•DK=AC•DH的理由吗?
如图,AD是△ABC的角平分线,BH⊥AD,CK⊥AD,垂足分别为点H、K,你能说明AB•DK=AC•DH的理由吗?
解:∵AD是△ABC的角平分线,
∴∠BAH=∠CAK,
∵BH⊥AD,CK⊥AD,
∴∠AHB=∠K=90°,BH∥CK,
∴△ABH∽△ACK,△BDH∽△CDK,
∴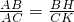 ,
,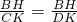 ,
,
∴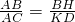 ,
,
∴AB•DK=AC•DH.
分析:由AD是△ABC的角平分线,BH⊥AD,CK⊥AD,易证得△ABH∽△ACK,△BDH∽△CDK,然后由相似三角形的对应边成比例,易证得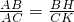 ,
,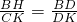 ,继而可得AB•DK=AC•DH.
,继而可得AB•DK=AC•DH.
点评:此题考查了相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.
∴∠BAH=∠CAK,
∵BH⊥AD,CK⊥AD,
∴∠AHB=∠K=90°,BH∥CK,
∴△ABH∽△ACK,△BDH∽△CDK,
∴
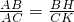 ,
,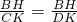 ,
,∴
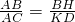 ,
,∴AB•DK=AC•DH.
分析:由AD是△ABC的角平分线,BH⊥AD,CK⊥AD,易证得△ABH∽△ACK,△BDH∽△CDK,然后由相似三角形的对应边成比例,易证得
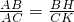 ,
,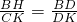 ,继而可得AB•DK=AC•DH.
,继而可得AB•DK=AC•DH.点评:此题考查了相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目

 如图,AD是△ABC是角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G,则AD与EF的位置关系是
如图,AD是△ABC是角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G,则AD与EF的位置关系是 16、已知:如图,AD是△ABC的角平分线,且 AB:AC=3:2,则△ABD与△ACD的面积之比为
16、已知:如图,AD是△ABC的角平分线,且 AB:AC=3:2,则△ABD与△ACD的面积之比为 如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm.
如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm. 如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )
如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )