题目内容
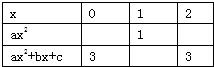
已知下表:
|
x |
0 |
1 |
2 |
|
ax2 |
|
1 |
|
|
ax2+bx+c |
3 |
|
3 |
(1)求a、b、c的值,并在表内空格处填入正确的数;
(2)请你根据上面的结果判断:
①是否存在实数x,使二次三项式ax2+bx+c的值为0?若存在,求出这个实数值;若不存在,请说明理由.
②画出函数y=ax2+bx+c的图象示意图,由图象确定,当x取什么实数时,ax2+ bx+c>0?
【答案】
(1) a=1,b=-2,c=3,空格内分别应填入0,4,2. (2) ①不存在②无论x取什么实数总有ax2+bx+c>0.
【解析】本题主要考查了二次函数与不等式(组).
(1)设函数的解析式为:y=ax2+bx+c,由图中表格知,当x=0时,y=3,当x=2时y=3,函数对抽为x=1,根据待定系数法求出函数的解析式,从而求解;
(2)根据方程的△与0的关系来判断是否存在;根据五点作图法画出二次函数的图象,从而求解.
(1)由表知,当x=0时,ax2+bx+c=3;当x=1时,ax2=1;当x=2时,ax2+bx+c=3.
∴ ,∴
,∴ ,
,
∴a=1,b=-2,c=3,空格内分别应填入0,4,2.
(2)①在x2-2x+3=0中,∵△=(-2)2-4×1×3=-8<0,
∴不存在实数x能使ax2+bx+c=0.
②函数y=x2-2x+3的图象示意图如答图所示,

观察图象得出,无论x取什么实数总有ax2+bx+c>0.

练习册系列答案
相关题目
 已知下表:
已知下表: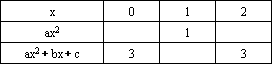
 已知下表:
已知下表: