题目内容
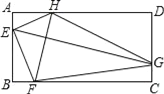
【题目】已知:如图,∠DAE=∠E,∠B=∠D,试说明AB与DC平行.

解:因为∠DAE=∠E,(已知)
所以____∥____(_______)
所以∠D=____(_______)
因为∠B=∠D,(已知)
所以∠B=∠____(_______)
所以____∥____(_______)
【答案】AD;BE;内错角相等,两直线平行;∠DCE;两直线平行,内错角相等;∠DCE;等量代换;AB;CD;同位角相等,两直线平行.
【解析】
因为∠DAE=∠E,所以根据内错角相等,两直线平行,可以证明AD∥BE;根据平行线的性质,可得∠D=∠DCE,结合已知条件,运用等量代换,可得∠B=∠DCE,可证明AB∥DC.
解:∵∠DAE=∠E,(已知)∴AD∥BE,(内错角相等,两直线平行)∴∠D=∠DCE,(两条直线平行,内错角相等)∵∠B=∠D,(已知)∴∠B=∠DCE,(等量代换)∴AB∥DC(同位角相等,两条直线平行).

练习册系列答案
相关题目