题目内容
如图，△ABC为等腰三角形，AB=AC，O是底边BC的中点，⊙O与腰AB相切于点D，
求证AC与⊙O
相切。
.证明：连结OD，过点O作OE⊥AC于E点，∵AB切⊙O于D，∴OD⊥AB．∴∠ODB=∠OEC=90°．又∵O是
BC的中点，∴OB=OC．∵AB=AC，∴∠B=∠C．∴△OBE≌△OCE．∴OE=OD，即OE是⊙O的半径．∴AC
与⊙O相切．
解析
练习册系列答案
相关题目
2、如图，△ABC为等腰三角形，AB=AC，∠A=40°，D，E，F分别在BC，AC，AB上，且CE=CD，BD=BF，则∠EDF的度数为（ ）
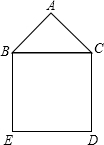如图，△ABC为等腰直角三角形，它的面积为8平方厘米，以它的斜边为边的正方形BCDE的面积为（ ）平方厘米．| A、16 | B、24 | C、64 | D、32 |
如图，△ABC为等腰直角三角形∠BAC=90°，AD是斜边BC上的中线，△ABD旋转到△ACE的位置．
（2013•六合区一模）如图，△ABC为等腰直角三角形，∠C=90°，若在某一平面直角坐标系中，顶点C的坐标为（1，1），B的坐标为（2，0）．则顶点A的坐标是（ ）
如图，△ABC为等腰三角形，如果把它沿底边BC翻折后，得到△DBC，那么四边形ABDC为（ ）