题目内容
（本题12分）计算
（1）4.8－（－1.2）＋（－6） （2）
×
÷
（3）1－
÷
（4）－
×
－
【答案】
（1）0； （2）
； （3）
（4）-14
【解析】
试题分析：
（1）4.8－（－1.2）＋（－6） （2）
×
÷
=4.8+1.2-6
=
×（-
）×（-
）
=0
=--
（3）1－
÷
（4）－
×
－
=1－（-2）×（-
）
=-36×
-8
=1-
=-6-8
=
=-14
考点：有理数的运算
点评：此种试题，主要考查学生对有理数运算的规则：先算幂，再算乘除，后算加减，有括号的要先算括号里面的。
练习册系列答案
阅读快车系列答案
相关题目
（本题12分）某商场购进一批单价为5元的日用商品.如果以单价7元销售，每天可售出160件.根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高1元，销售量每天就相应减少20件.设这种商品的销售单价为x元，商品每天销售这种商品所获得的利润为y元.
（1）给定x的一些值，请计算y的一些值.
（2）求y与x之间的函数关系式，并探索：当商品的销售单价定为多少元时，该商店销售这种商品获得的利润最大？这时每天销售的商品是多少件？
（1）给定x的一些值，请计算y的一些值.
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … | | | | | | … |
﹣（本题12分）在一平直河岸
同侧有
两个村庄，到的距离分别是3km和2km，
．现计划在河岸上建一抽水站
，用输水管向两个村庄供水．
方案设计
某班数学兴趣小组设计了两种铺设管道方案：图（1）是方案一的示意图，设该方案中管道长度为
，且
（其中
于点）；图（2）是方案二的示意图，设该方案中管道长度为
，且
（其中点
与点
关于对称，
与交于点）．
（1）观察计算
在方案一中，
km（用含
的式子表示）；
在方案二中，组长小宇为了计算的长，作了如图（3）所示的辅助线，请你按小宇同学的思路计算，
km（用含的式子表示）．
（2）探索归纳
①当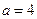
时，比较大小：
（填“＞”、“＝”或“＜”）；
当
时，比较大小：（填“＞”、“＝”或“＜”）；
②请你参考右边方框中的方法指导，
就（当
时）的所有取值情况进
行分析，要使铺设的管道长度较短，
应选择方案一还是方案二？
同侧有两个村庄，到的距离分别是3km和2km，．现计划在河岸上建一抽水站，用输水管向两个村庄供水．方案设计
某班数学兴趣小组设计了两种铺设管道方案：图（1）是方案一的示意图，设该方案中管道长度为
，且（其中于点）；图（2）是方案二的示意图，设该方案中管道长度为，且（其中点与点关于对称，与交于点）． |
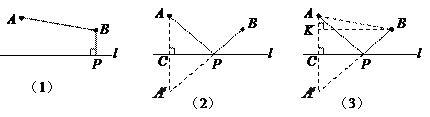（1）观察计算
在方案一中，
km（用含的式子表示）；在方案二中，组长小宇为了计算
的长，作了如图（3）所示的辅助线，请你按小宇同学的思路计算， km（用含的式子表示）．（2）探索归纳
①当
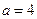时，比较大小：（填“＞”、“＝”或“＜”）；当
时，比较大小：（填“＞”、“＝”或“＜”）；②请你参考右边方框中的方法指导，就
（当时）的所有取值情况进行分析，要使铺设的管道长度较短，
应选择方案一还是方案二？
×
÷
÷
（4）－
×
－
