Question

已知，如图，点C在线段AB上，在AB的同旁作等边△ADC和等边△BCE，连接AE、BD交CD、CE于M、N，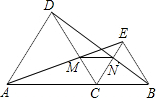
（1）求证：AE=BD；
（2）求证：△CMN为等边三角形；
（3）如果把△BEC绕着C点旋转任意角度，上述结论中哪些成立？试说明理由．

Answer 1

分析：（1）根据等边三角形性质推出AC=CD，BC=CE，∠DCA=∠ECB=60°，求出∠ACE=∠DCB，根据SAS证△ACE≌△DCB即可；
（2）求出∠ECD=60°，推出∠AEC=∠DBC，证△EMC≌△BNC，推出CN=CM即可．
（3）结论（1）正确，根据（1）的推理过程即可得出答案．

解答：（1）证明：∵等边△ADC和△BCE，
∴AC=CD，BC=CE，∠DCA=∠ECB=60°，
∴∠DCA+∠DCE=∠ECB+∠DCE，
∴∠ACE=∠DCB，
在△ACE和△DCB中

AC=DC ∠ACE=∠DCB CE=BC

，
∴△ACE≌△DCB，
∴AE=BD．

（2）证明：∵△ACE≌△DCB，
∴∠DBC=∠AEC，
∵∠DCE=180°-∠ACD-∠BCE=60°=∠BCE，
在△EMC和△BNC中

∠ECB=∠ECM ∠AEC=∠CBD EC=BC

，
∴△EMC≌△BNC，
∴CM=CN，
∵∠MCN=60°，
∴△CMN是等边三角形．

（3）结论（1）成立，
理由是：不论旋转多少度，AC=CD，BC=CE，∠DCA=∠ECB=60°，
推出∠ACE=∠BCD，
∴△ACE≌△DCB，
∴AE=BD．

点评：本题考查了对全等三角形的性质和判定，等边三角形的性质和判定的应用，主要培养学生运用性质进行推理的能力．