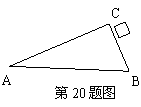题目内容
 如图,已知BD是三角形ABC外接圆直径,连接CD,若DC=12,BD=13,则cosA的值是( )
如图,已知BD是三角形ABC外接圆直径,连接CD,若DC=12,BD=13,则cosA的值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由圆周角定理知:∠A=∠D,因此只需求出∠D的余弦值即可.
Rt△BDE中,已知了CD和BD的长,即可求出∠D的余弦值,由此得解.
Rt△BDE中,已知了CD和BD的长,即可求出∠D的余弦值,由此得解.
解答:解:∵BD是⊙O的直径,
∴∠BCD=90°.
Rt△BCD中,CD=12,BD=13,
∴cos∠D=
=
.
∵∠A=∠D,
∴cos∠A=
.
故选C.
∴∠BCD=90°.
Rt△BCD中,CD=12,BD=13,
∴cos∠D=
| CD |
| BD |
| 12 |
| 13 |
∵∠A=∠D,
∴cos∠A=
| 12 |
| 13 |
故选C.
点评:此题综合考查了圆周角定理以及锐角三角函数的概念.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 ,则等边三角
,则等边三角
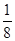 B.
B.  C.
C.
 D.1
D.1