题目内容
某花木基地的A、B、C三种名贵花苗,每株的销售价格分别为3元、2元、1元.在一次出售花苗时,销售A、B两种花苗株数的比为1:2;销售B、C两种花苗的株数的比为3:4,共获销售金额29000元,那么,此次销售A、B、C三种花苗共________株.
17000
分析:首先假设此次销售A、B、C三种花苗依次是x株,y株,z株.根据销售A、B两种花苗株数的比为1:2列出方程 ,根据销售B、C两种花苗的株数的比为3:4列出方程
,根据销售B、C两种花苗的株数的比为3:4列出方程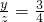 ,根据共获销售金额29000元列出方程3x+2y+z=29000.利用代入消元法解方程组即可求得x、y、z的值,x+y+z的值也就确定.最终问题得解.
,根据共获销售金额29000元列出方程3x+2y+z=29000.利用代入消元法解方程组即可求得x、y、z的值,x+y+z的值也就确定.最终问题得解.
解答:设此次销售A、B、C三种花苗依次是x株,y株,z株.
根据题意得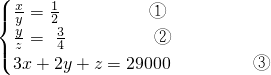
由①得x=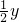 ④
④
由②得z= ⑤
⑤
将④⑤代入③解得 y=6000,则x=3000,z=8000
此次销售A、B、C三种花苗共6000+3000+8000=17000(株)
故答案为17000.
点评:解答此题的关键是列出方程组,用代入消元法或加减消元法求出方程组的解.
分析:首先假设此次销售A、B、C三种花苗依次是x株,y株,z株.根据销售A、B两种花苗株数的比为1:2列出方程
 ,根据销售B、C两种花苗的株数的比为3:4列出方程
,根据销售B、C两种花苗的株数的比为3:4列出方程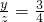 ,根据共获销售金额29000元列出方程3x+2y+z=29000.利用代入消元法解方程组即可求得x、y、z的值,x+y+z的值也就确定.最终问题得解.
,根据共获销售金额29000元列出方程3x+2y+z=29000.利用代入消元法解方程组即可求得x、y、z的值,x+y+z的值也就确定.最终问题得解.解答:设此次销售A、B、C三种花苗依次是x株,y株,z株.
根据题意得
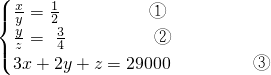
由①得x=
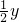 ④
④由②得z=
 ⑤
⑤将④⑤代入③解得 y=6000,则x=3000,z=8000
此次销售A、B、C三种花苗共6000+3000+8000=17000(株)
故答案为17000.
点评:解答此题的关键是列出方程组,用代入消元法或加减消元法求出方程组的解.

练习册系列答案
相关题目