题目内容
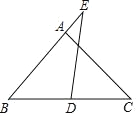
如图,在Rt△ABC中,∠BAC=90°,AB=AC=4,D是BC的中点,点E在BA的延长线上,连接ED,若AE=2,则DE的长为_____.
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
题目内容
如图,在Rt△ABC中,∠BAC=90°,AB=AC=4,D是BC的中点,点E在BA的延长线上,连接ED,若AE=2,则DE的长为_____.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案