题目内容
 (2012•长春一模)如图,四边形ABCD是矩形,以AD为直径的⊙O交BC边于点E、F,AB=4,AD=12.求线段EF的长.
(2012•长春一模)如图,四边形ABCD是矩形,以AD为直径的⊙O交BC边于点E、F,AB=4,AD=12.求线段EF的长.分析:作OM⊥BC于M,连接OE,根据垂径定理求出EF=2EM,求出OE和OM长,根据勾股定理求出EM,即可求出EF.
解答:解:作OM⊥BC于M,连接OE,
则ME=MF=
EF,
∵AD=12,
∴OE=6,
在矩形ABCD中,OM⊥BC,
∴OM=AB=4,
∵在△OEM中,∠OME=90°,
ME=
=
=2
,
∴线段EF的长度为4
.

则ME=MF=
| 1 |
| 2 |
∵AD=12,
∴OE=6,
在矩形ABCD中,OM⊥BC,
∴OM=AB=4,
∵在△OEM中,∠OME=90°,
ME=
| OE2-OM2 |
=
| 62-42 |
=2
| 5 |
∴线段EF的长度为4
| 5 |
点评:本题考查了勾股定理、垂径定理、矩形的性质等知识点,关键是构造直角三角形,题目比较典型,是一道比较好的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
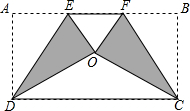 (2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则
(2012•长春一模)将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则 (2012•长春一模)如图,抛物线y=ax2-x-
(2012•长春一模)如图,抛物线y=ax2-x- -B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)
-B于点P,以PQ为一边向右作正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形OABC重叠面积为S(平方单位)